【題目】某公司租地建倉庫，每月土地占用費y1與車庫到車站的距離x成反比，而每月的庫存貨物的運費y2與車庫到車站的距離x成正比．如果在距離車站10公里處建立倉庫，這兩項費用y1和y2分別為2萬元和8萬元．求若要使得這兩項費用之和最小時，倉庫應建在距離車站多遠處？此時最少費用為多少萬元？
【答案】解：設 
，y2=k2x，由題意可得： 
，8=10k2 ， 解得k1=20， 
．設這兩項費用之和為f（x），則f（x）= 
+ 
．
∵x＞0，∴f（x） 
=8，
當且僅當 
，解得x=5時取得等號．
答：若要使得這兩項費用之和最小時，倉庫應建在距離車站8公里處，此時最少費用為8萬元．
【解析】設 
，y2=k2x，由題意可得： 
，8=10k2 ， 解得k1 ， k2 ． 設這兩項費用之和為f（x），則f（x）= 
．利用基本不等式即可得出．
【考點精析】關于本題考查的基本不等式在最值問題中的應用，需要了解用基本不等式求最值時（積定和最小，和定積最大），要注意滿足三個條件“一正、二定、三相等”才能得出正確答案．
科目：高中數學 來源： 題型：
【題目】若不等式（m﹣1）x2+（m﹣1）x+2＞0的解集是R，則m的范圍是（ ）
A.（1，9）
B.（﹣∞，1]∪（9，+∞）
C.[1，9）
D.（﹣∞，1）∪（9，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4—4:坐標系與參數方程
在平面直角坐標系
中，曲線
的參數方程為
(其中
為參數）.以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系并取相同的單位長度，曲線
的極坐標方程為
.
（1）把曲線
的方程化為普通方程， 
的方程化為直角坐標方程；
（2）若曲線
， 
相交于
兩點， 
的中點為
，過點
做曲線
的垂線交曲線
于
兩點，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2+bx+c．
（1）若a＞b＞c，且f（1）=0，證明f（x）的圖象與x軸有2個交點；
（2）在（1）的條件下，是否存在m∈R，使得f（m）=﹣a成立時，f（m+3）為正數，若存在，證明你的結論，若不存在，請說明理由；
（3）若對x1 ， x2∈R，且x1＜x2 ， f（x1）≠f（x2），方程f（x）= 
[f（x1）+f（x2）]有兩個不等實根，證明必有一個根屬于（x1 ， x2）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知圓
及點
， 
．
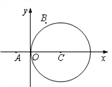
(1)若直線
平行于
，與圓
相交于
， 
兩點， 
，求直線
的方程；
（2）在圓C上是否存在點P,使得
?若存在，求點P的個數；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
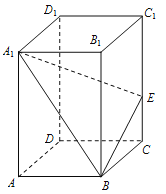
【題目】如圖，已知長方體ABCD－A1B1C1D1中，AB＝3，BC＝2，CC1＝5，E是棱CC1上不同于端點的點，且
．
（1） 當∠BEA1為鈍角時，求實數λ的取值范圍；
（2） 若λ＝
，記二面角B1－A1B－E的的大小為θ，求|cosθ|．
查看答案和解析>>
科目：高中數學 來源： 題型：
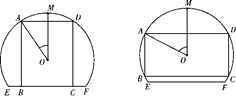
【題目】如圖，一塊弓形余布料EMF，點M為弧
的中點，其所在圓O的半徑為4 dm（圓心O在弓形EMF內），∠EOF=
．將弓形余布料裁剪成盡可能大的矩形ABCD(不計損耗)， AD∥EF，且點A、D在弧
上，設∠AOD=
．
（1）求矩形ABCD的面積S關于
的函數關系式；
（2）當矩形ABCD的面積最大時，求cos
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班有24名男生和26名女生，數據a1 ， a2 ， …，a50是該班50名學生在一次數學學業水平模擬考試的成績，下面的程序用來同時統計全班成績的平均數：A，男生平均分：M，女生平均分：W；為了便于區別性別，輸入時，男生的成績用正數，女生的成績用其成績的相反數，那么在圖里空白的判斷框和處理框中，應分別填入下列四個選項中的（ ）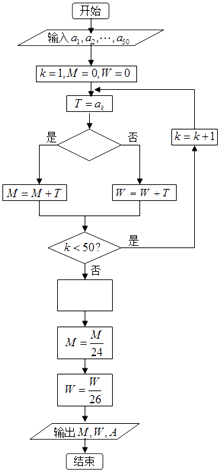 
A.T＞0？， 
B.T＜0？， ??
C.T＜0？， 
D.T＞0？，
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
