
【題目】給出下列四個(gè)命題: ①若a<b,則a2<b2;
②若a≥b>﹣1,則 ![]() ≥
≥ ![]() ;
;
③若正整數(shù)m和n滿足m<n,則 ![]() ≤
≤ ![]() ;
;
④若x>0,且x≠1,則lnx+ ![]() ≥2.
≥2.
其中所有真命題的序號是

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時(shí),求證:
時(shí),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() ,
,![]() ,則函數(shù)
,則函數(shù)![]() 的圖像經(jīng)過怎樣的變換可以得到函數(shù)
的圖像經(jīng)過怎樣的變換可以得到函數(shù)![]() 的圖像
的圖像
①先向左平移![]() 個(gè)單位,再將橫坐標(biāo)縮短到原來的
個(gè)單位,再將橫坐標(biāo)縮短到原來的![]() 倍,縱坐標(biāo)保持不變.
倍,縱坐標(biāo)保持不變.
②先向左平移![]() 個(gè)單位,再將橫坐標(biāo)縮短到原來的
個(gè)單位,再將橫坐標(biāo)縮短到原來的![]() 倍,縱坐標(biāo)保持不變.
倍,縱坐標(biāo)保持不變.
③將橫坐標(biāo)縮短到原來的![]() 倍,再向左平移
倍,再向左平移![]() 個(gè)單位,縱坐標(biāo)保持不變.
個(gè)單位,縱坐標(biāo)保持不變.
④將橫坐標(biāo)縮短到原來的![]() 倍,再向左平移
倍,再向左平移![]() 個(gè)單位,縱坐標(biāo)保持不變.
個(gè)單位,縱坐標(biāo)保持不變.
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】袋子中放有大小和形狀相同而顏色互不相同的小球若干個(gè), 其中標(biāo)號為0的小球1個(gè), 標(biāo)號為1的小球1個(gè), 標(biāo)號為2的小球2個(gè), 從袋子中不放回地隨機(jī)抽取2個(gè)小球, 記第一次取出的小球標(biāo)號為![]() ,第二次取出的小球標(biāo)號為
,第二次取出的小球標(biāo)號為![]() .
.
(1) 記事件![]() 表示“
表示“![]() ”, 求事件
”, 求事件![]() 的概率;
的概率;
(2) 在區(qū)間![]() 內(nèi)任取2個(gè)實(shí)數(shù)
內(nèi)任取2個(gè)實(shí)數(shù)![]() , 記
, 記![]() 的最大值為
的最大值為![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的準(zhǔn)線方程為
的準(zhǔn)線方程為![]() ,點(diǎn)
,點(diǎn)![]() 為坐標(biāo)原點(diǎn),不過點(diǎn)
為坐標(biāo)原點(diǎn),不過點(diǎn)![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() .
.
(1)如果直線![]() 過點(diǎn)
過點(diǎn)![]() ,求證:
,求證:![]() ;
;
(2)如果![]() ,證明:直線
,證明:直線![]() 必過一定點(diǎn),并求出該定點(diǎn).
必過一定點(diǎn),并求出該定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】小明和爸爸媽媽、爺爺奶奶一同參加《中國詩詞大會》的現(xiàn)場錄制,5人坐成一排.若小 明的父母至少有一人與小明相鄰,則不同的坐法總數(shù)為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)從某醫(yī)院中隨機(jī)抽取了7位醫(yī)護(hù)人員的關(guān)愛患者考核分?jǐn)?shù)(患者考核:10分制),用相關(guān)的特征量![]() 表示;醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)(試卷考試:100分制),用相關(guān)的特征量
表示;醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)(試卷考試:100分制),用相關(guān)的特征量![]() 表示,數(shù)據(jù)如下表:
表示,數(shù)據(jù)如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程(計(jì)算結(jié)果精確到0.01);
的線性回歸方程(計(jì)算結(jié)果精確到0.01);
(2)利用(1)中的線性回歸方程,分析醫(yī)護(hù)專業(yè)考核分?jǐn)?shù)的變化對關(guān)愛患者考核分?jǐn)?shù)的影響,并估計(jì)某醫(yī)護(hù)人員的醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)為95分時(shí),他的關(guān)愛患者考核分?jǐn)?shù)(精確到0.1)
附:回歸直線方程![]() 中斜率和截距的最小二乘法估計(jì)公式分別為
中斜率和截距的最小二乘法估計(jì)公式分別為
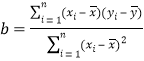 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)y=f(x)與y=g(x)的圖象如圖所示,則函數(shù)y=f(x)g(x)的圖象可能是( ) 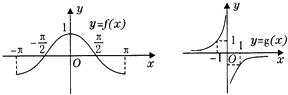
A.
B.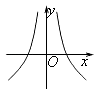
C.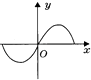
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1)(x∈R).
=(cosx,1)(x∈R).
(1)求f(x)的周期和單調(diào)遞減區(qū)間;
(2)在△ABC 中,角A、B、C的對邊分別為a,b,c,f(A)=﹣1,a= ![]() ,
, ![]()
![]() =3,求邊長b和c的值(b>c).
=3,求邊長b和c的值(b>c).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com