【題目】函數y=f（x）與y=g（x）的圖象如圖所示，則函數y=f（x）g（x）的圖象可能是（ ）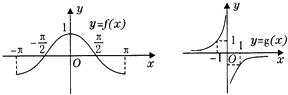 
A.
B.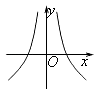
C.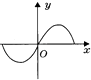
D.
【答案】A
【解析】解：∵y=f（x）的有兩個零點，并且g（x）沒有零點； ∴函數y=f（x）g（x）也有兩個零點M，N，
又∵x=0時，函數值不存在
∴y在x=0的函數值也不存在
當x∈（﹣∞，M）時，y＜0；
當x∈（M，0）時，y＞0；
當x∈（0，N）時，y＜0；
當x∈（N，+∞）時，y＞0；
只有A中的圖象符合要求
故選：A
本題考查的知識點是函數的圖象，由已知中函數y=f（x）與y=g（x）的圖象我們不難分析，當函數y=f（x）g（x）有兩個零點M，N，我們可以根據函數y=f（x）與y=g（x）的圖象中函數值的符號，分別討論（﹣∞，M）（M，0）（0，N）（N，+∞）四個區間上函數值的符號，以確定函數的圖象．
科目：高中數學 來源： 題型：
【題目】設函數y=lg（﹣x2+4x﹣3）的定義域為A，函數y= 
，x∈（0，m）的值域為B．
（1）當m=2時，求A∩B；
（2）若“x∈A”是“x∈B”的必要不充分條件，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題： ①若a＜b，則a2＜b2；
②若a≥b＞﹣1，則 
≥ 
；
③若正整數m和n滿足m＜n，則 
≤ 
；
④若x＞0，且x≠1，則lnx+ 
≥2．
其中所有真命題的序號是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=x3﹣ax﹣b，x∈R，其中a，b∈R． （Ⅰ）求f（x）的單調區間；
（Ⅱ）若f（x）存在極值點x0 ， 且f（x1）=f（x0），其中x1≠x0；求證：x1+2x0=0．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[2019·濰坊期末]某鋼鐵加工廠新生產一批鋼管，為了了解這批產品的質量狀況，檢驗員隨機抽取了100件鋼管作為樣本進行檢測，將它們的內徑尺寸作為質量指標值，由檢測結果得如下頻率分布表和頻率分布直方圖：
分組 | 頻數 | 頻率 |
25.05～25.15 | 2 | 0.02 |
25.15～25.25 | ||
25.25～25.35 | 18 | |
25.35～25.45 | ||
25.45～25.55 | ||
25.55～25.65 | 10 | 0.1 |
25.65～25.75 | 3 | 0.03 |
合計 | 100 | 1 |
（1）求
，
；
（2）根據質量標準規定：鋼管內徑尺寸大于等于25.75或小于25.15為不合格，鋼管尺寸在
或
為合格等級，鋼管尺寸在
為優秀等級，鋼管的檢測費用為0.5元/根．
（i）若從
和
的5件樣品中隨機抽取2根，求至少有一根鋼管為合格的概率；
（ii）若這批鋼管共有2000根，把樣本的頻率作為這批鋼管的頻率，有兩種銷售方案：
①對該批剩余鋼管不再進行檢測，所有鋼管均以45元/根售出；
②對該批剩余鋼管一一進行檢測，不合格產品不銷售，合格等級的鋼管50元/根，優等鋼管60元/根．
請你為該企業選擇最好的銷售方案，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設圓C滿足：①截y軸所得弦長為2；②被x軸分成兩段圓弧，其弧長的比為3:1，在滿足條件①、②的所有圓中，求圓心到直線l:x-2y=0的距離最小的圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（sin（A﹣B）， 
， 
=（1，2sinB），且 =﹣sin2C，其中A、B、C分別為△ABC的三邊a、b、c所對的角． （Ⅰ）求角C的大小；
（Ⅱ）若 
，且S△ABC= 
，求邊c的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數{an}滿a1=0，an+1=an+2n，那a2016的值是（ ）
A.2014×2015
B.2015×2016
C.2014×2016
D.2015×2015
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=AA1=1，延長A1C1至點P，使C1P=A1C1 ， 連接AP交棱CC1于點D． （Ⅰ）求證：PB1∥平面BDA1；
（Ⅱ）求二面角A﹣A1D﹣B的平面角的余弦值．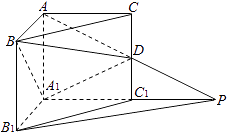
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com