
【題目】已知函數![]() ,
, ![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,判斷方程
時,判斷方程![]() 在區間
在區間![]() 上有無實根;
上有無實根;
(3)若![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;(2) 內無實數根;(3)
;(2) 內無實數根;(3)![]() .
.
【解析】試題分析:(2)把m的值代入后,求出f(1),求出x=1時函數的導數,由點斜式寫出曲線y=f(x)在點(1,f(1))處的切線方程;
(Ⅱ)代入m的值,把判斷方程f(x)=g(x)在區間(1,+∞)上有無實根轉化為判斷函數h(x)=f(x)﹣g(x)在(1,+∞)上有無零點問題,求導后利用函數的單調性即可得到答案;
(Ⅲ)把f(x)和g(x)的解析式代入不等式,整理變形后把參數m分離出來,x∈(1,e]時,不等式f(x)﹣g(x)<2恒成立,轉化為實數m小于一個函數在(1,e]上的最小值,然后利用導數分析函數在(1,e]上的最小值.
試題解析:
(1)![]() 時,
時, ![]() ,
, ![]() ,
, ![]() ,切點坐標為
,切點坐標為![]() ,
,
∴切線方程為![]()
(2)![]() 時,令
時,令![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 上為增函數,
上為增函數,
又![]() ,所以
,所以![]() 在
在![]() 內無實數根.
內無實數根.
(3)![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
又![]() ,則當
,則當![]() 時,
時, ![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() 小于
小于![]() 的最小值.
的最小值.
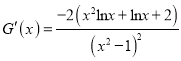 ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,∴
上單調遞減,∴![]() 在
在![]() 的最小值為
的最小值為![]() ,
,
則![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某次考試后,對全班同學的數學成績進行整理,得到表:
分數段 |
|
|
|
|
人數 | 5 | 15 | 20 | 10 |
將以上數據繪制成頻率分布直方圖后,可估計出本次考試成績的中位數是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2α﹣4cosα=0.已知直線l的參數方程為![]() (
(![]() 為參數),點M的直角坐標為
為參數),點M的直角坐標為![]() .
.
(1)求直線l和曲線C的普通方程;
(2)設直線l與曲線C交于A,B兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018屆安徽省蚌埠市高三上學期第一次教學質量檢查】為監控某種零件的一條生產線的生產過程,檢驗員每天從該生產線上隨機抽取10件零件,度量其內徑尺寸(單位: ![]() ).根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件的內徑尺寸服從正態分布
).根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件的內徑尺寸服從正態分布![]() .
.
(1)假設生產狀態正常,記![]() 表示某一天內抽取的10個零件中其尺寸在
表示某一天內抽取的10個零件中其尺寸在![]() 之外的零件數,求
之外的零件數,求![]() 及
及![]() 的數學期望;
的數學期望;
(2)某天正常工作的一條生產線數據記錄的莖葉圖如下圖所示:
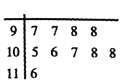
①計算這一天平均值![]() 與標準差
與標準差![]() ;
;
②一家公司引進了一條這種生產線,為了檢查這條生產線是否正常,用這條生產線試生產了5個零件,度量其內徑分別為(單位: ![]() ):85,95,103,109,119,試問此條生產線是否需要進一步調試,為什么?
):85,95,103,109,119,試問此條生產線是否需要進一步調試,為什么?
參考數據: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的右焦點
的右焦點![]() 與短軸兩個端點的連線互相垂直.
與短軸兩個端點的連線互相垂直.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 為橢圓
為橢圓![]() 的上一點,過原點
的上一點,過原點![]() 且垂直于
且垂直于![]() 的直線與直線
的直線與直線![]() 交于點
交于點![]() ,求
,求![]() 面積
面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法錯誤的是( )
A. 若“![]() ”為假命題,則p,q均為假命題
”為假命題,則p,q均為假命題
B. “ ![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
C. “![]() ”的必要不充分條件是“
”的必要不充分條件是“![]() ”
”
D. 若命題p:![]() ,
,![]() ,則命題
,則命題![]() :
:![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com