【題目】已知函數
是定義在R上的奇函數，當
時，
(1) 求
和
的值；
(2)求函數的解析式
【答案】（1）f（0）＝0，
，（2）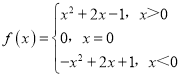
【解析】
（1）由奇函數的性質得出f（﹣x）＝﹣f（x），令x＝0，-3代入可求f（0），
；
（2）設x＜0，從而﹣x＞0，代入當x＞0時的表達式f（x）＝x2+2x-1可得x＜0時的表達式．
（1）∵函數f（x）是定義在R上的奇函數，∴f（﹣x）＝﹣f（x），
∴f（﹣0）＝﹣f（0），f（0）＝﹣f（0）
∴f（0）＝0；
而
，
∴f（0）＝0，；
（2）設x＜0，∴﹣x＞0，
又當x＞0時，f（x）＝x2+2x﹣1．
∴f（﹣x）＝（﹣x）2+2（﹣x）﹣1＝x2﹣2x﹣1，
∴﹣f（x）＝x2﹣2x﹣1，
∴f（x）＝﹣x2+2x+1，
∴當x＜0時，f（x）＝﹣x2+2x+1，
又由（1）知f（0）＝0
∴
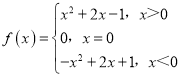
核心素養學練評系列答案
單元期中期末卷系列答案科目：高中數學 來源： 題型：
【題目】已知二次函數
的圖像經過點
，且滿足
，
(1)求
的解析式；
(2)已知
，求函數
在
的最大值和最小值；
函數
的圖像上是否存在這樣的點，其橫坐標是正整數，縱坐標是一個完全平方數？如果存在，求出這樣的點的坐標；如果不存在，請說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】口袋里共有4個球，其中有2個是白球，2個是黑球，這4個球除顏色外完全相同。4個人按順序依次從中摸出一個球（不放回），試計算第二個人摸到白球的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
：
（1）若
，求y＝f（x）的最大值和最小值，并寫出相應的x值；
（2）將函數y＝f（x）的圖象向右平移
個單位，再向上平移1個單位，得到函數y＝g（x）的圖象，區間[a，b]（a，b∈R且a＜b）滿足：y＝g（x）在[a，b]上至少含有20個零點，在所有滿足上述條件的[a，b]中，求b﹣a的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一容量為200的樣本，數據的分組以及各組的頻數如下：
，7；
，11；
，15；
，40；
，49；
，41；
，20；
，17.
（1）列出樣本的頻率分布表；
（2）畫出頻率分布直方圖和頻率分布折線圖；
（3）求樣本數據不足0的頻率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
