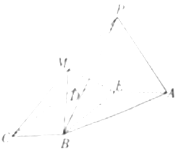
【題目】如圖，我海監船在
島海域例行維權巡航，某時刻航行至
處，此時測得其東北方向與它相距32海里的
處有一外國船只，且
島位于海監船正東
海里處．
（1）求此時該外國船只與島的距離；
（2）觀測中發現，此外國船只正以每小時8海里的速度沿正南方向航行，為了將該船攔截在離島24海里處，不讓其進入島24海里內的海域，試確定海監船的航向，并求其速度的最小值．（參考數據：
）
【答案】（1）
；（2）
.
【解析】
試題分析：（1）直接利用余弦定理，求得距離為
；（2）過點
作
于點
，連結
，利用勾股定理和正弦的概念，求得
，故海監船的航向為北偏東
，同時，外國船只到達點
的時間
（小時），海監船的速度
.
試題解析：
（1）依題意，在
中，
，
由余弦定理得
，
∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分
即此時該外國船只與
島的距離為海里．．．．．．．．．．．．．．．．．．．．．5分
（2）過點作于點，
在
中，
，∴
，．．．．．．．．．．6分
以
為圓心，24為半徑的圓交
于點
，連結，
在
中，
，∴
．．．．．．．．．．．．．．．．．7分
又
，
∴
．．．．．．．．．．．．．．．．．9分
外國船只到達點的時間（小時）
∴海監船的速度（海里/小時）．．．．．．．．．．．．．．．．．．11分
故海監船的航向為北偏東，速度的最小值為40海里/小時．．．．．．．．．．12分
優生樂園系列答案科目：高中數學 來源： 題型：
【題目】設等差數列
是無窮數列，且各項均為互不相同的正整數，其前
項和為
，數列
滿足
.
（1）若
，求
的值；
（2）若數列
為等差數列，求
；
（3）在（1）的條件下，求證：數列
中存在無窮多項（按原來的順序）成等比數列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若對于定義在
上的連續函數
，存在常數
（
），使得
對任意的實數
成立，則稱
是回旋函數，且階數為
.
（1）試判斷函數
是否是一個階數為1的回旋函數，并說明理由；
（2）已知
是回旋函數，求實數
的值；
（3）若回旋函數
（
）在
恰有100個零點，求實數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）若
，判斷函數
的單調性；
（2）若函數
在定義域內單調遞減，求實數
的取值范圍；
（3）當
時，關于
的方程
在
上恰有兩個不相等的實數根，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面為直角梯形，
，平面
底面
，
為
的中點，
為正三角形，
是棱
上的一點(異于端點).
（Ⅰ）若為中點，求證：
平面
；
（Ⅱ）是否存在點，使二面角
的大小為30°.若存在，求出點的位置；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為確定下一年度投入某種產品的宣傳費，需了解年宣傳費
（單位：千元）對年利潤
（單位：萬元）的影響，對近5年的宣傳費
和年利潤
（
）進行了統計，列出了下表：
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
員工小王和小李分別提供了不同的方案．
（1）小王準備用線性回歸模型擬合
與
的關系，請你幫助建立
關于
的線性回歸方程；（系數精確到0.01）
（2）小李決定選擇對數回歸模型擬合
與
的關系，得到了回歸方程：
，并提供了相關指數
．請用相關指數說明選擇哪個模型更合適，并預測年宣傳費為4萬元的年利潤．（精確到0.01）（小王也提供了他的分析分析數據
）
參考公式：相關指數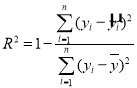
回歸方程
中斜率和截距的最小二乘估計公式分別為：
，
．參考數據：
，
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
