
【題目】讀下列所給程序,依據(jù)程序畫出程序框圖,并說明其功能.
INPUT “輸入三個正數(shù)a,b,c=”;a,b,c
IF a+b>c AND a+c>b AND b+c>a THEN
p=(a+b+c)/2
S=SQR(p*(p-a)*(p-b)*(p-c))
PRINT “三角形的面積S=”S
ELSE
PRINT “構不成三角形”
END IF
END.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】設某物體一天中的溫度![]() 是時間
是時間![]() 的函數(shù),已知
的函數(shù),已知![]() ,其中溫度的單位是
,其中溫度的單位是![]() ,時間的單位是小時,規(guī)定中午12:00相應的
,時間的單位是小時,規(guī)定中午12:00相應的![]() ,中午12:00以后相應的
,中午12:00以后相應的![]() 取正數(shù),中午12:00以前相應的
取正數(shù),中午12:00以前相應的![]() 取負數(shù)(例如早上8:00相應的
取負數(shù)(例如早上8:00相應的![]() ,下午16:00相應的
,下午16:00相應的![]() ),若測得該物體在中午12:00的溫度為
),若測得該物體在中午12:00的溫度為![]() ,在下午13:00的溫度為
,在下午13:00的溫度為![]() ,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
(1)求該物體的溫度![]() 關于時間
關于時間![]() 的函數(shù)關系式;
的函數(shù)關系式;
(2)該物體在上午10:00至下午14:00這段時間中(包括端點)何時溫度最高?最高溫度是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數(shù).當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當![]() 時,車流速度
時,車流速度![]() 是車流密度
是車流密度![]() 的一次函數(shù).
的一次函數(shù).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的表達式;
的表達式;
(2)當車流密度![]() 為多大時,車流量(單位時間內(nèi)通過橋上某觀測點的車輛數(shù),單位:輛/小時)
為多大時,車流量(單位時間內(nèi)通過橋上某觀測點的車輛數(shù),單位:輛/小時)![]() 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若函數(shù)![]() 在
在![]() 內(nèi)存在兩個極值點,求
內(nèi)存在兩個極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列程序運行后,a,b,c的值各等于什么?

(1)_____________________________________________________________.
(2)_____________________________________________________________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將圓![]() 上每一點的縱坐標不變,橫坐標變?yōu)樵瓉淼?/span>
上每一點的縱坐標不變,橫坐標變?yōu)樵瓉淼?/span>![]() ,得曲線C.
,得曲線C.
(Ⅰ)寫出C的參數(shù)方程;
(Ⅱ)設直線l: ![]() 與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
⑴求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
⑵如果對于任意的![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
⑶設函數(shù)![]() ,
, ![]() .過點
.過點![]() 作函數(shù)
作函數(shù)![]() 的圖象
的圖象
的所有切線,令各切點的橫坐標構成數(shù)列![]() ,求數(shù)列
,求數(shù)列![]() 的所有項之和
的所有項之和![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ![]()
(1)當a<0時,判斷f(x)在(0,+∞)上的單調性;
(2)當a=﹣4時,對任意的實數(shù)x1 , x2∈[1,2],都有f(x1)≤g(x2),求實數(shù)m的取值范圍;
(3)當 ![]() ,
, 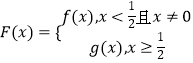 ,y=|F(x)|在(0,1)上單調遞減,求a的取值范圍.
,y=|F(x)|在(0,1)上單調遞減,求a的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com