Question

【題目】幾位大學生響應國家的創業號召，開發了一款應用軟件．為激發大家學習數學的興趣，他們推出了“解數學題獲取軟件激活碼”的活動．這款軟件的激活碼為下面數學問題的答案：已知數列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一項是20 ， 接下來的兩項是20 ， 21 ， 再接下來的三項是20 ， 21 ， 22 ， 依此類推．求滿足如下條件的最小整數N：N＞100且該數列的前N項和為2的整數冪．那么該款軟件的激活碼是（　　）
A.440
B.330
C.220
D.110

Answer 1

【答案】A
【解析】解：設該數列為{an}，設bn= +…+ =2n﹣1，（n∈N+），則 = ai ，
由題意可設數列{an}的前N項和為SN ， 數列{bn}的前n項和為Tn ， 則Tn=21﹣1+22﹣1+…+2n﹣1=2n﹣n﹣2，
可知當N為 時（n∈N+），數列{an}的前N項和為數列{bn}的前n項和，即為2n﹣n﹣2，
容易得到N＞100時，n≥14，
A項，由 =435，440=435+5，可知S440=T29+b5=230﹣29﹣2+25﹣1=230 ， 故A項符合題意．
B項，仿上可知 =325，可知S330=T25+b5=226﹣25﹣2+25﹣1=226+4，顯然不為2的整數冪，故B項不符合題意．
C項，仿上可知 =210，可知S220=T20+b10=221﹣20﹣2+210﹣1=221+210﹣23，顯然不為2的整數冪，故C項不符合題意．
D項，仿上可知 =105，可知S110=T14+b5=215﹣14﹣2+25﹣1=215+15，顯然不為2的整數冪，故D項不符合題意．
故選A．
方法二：由題意可知： ， ， ，… ，
根據等比數列前n項和公式，求得每項和分別為：21﹣1，22﹣1，23﹣1，…，2n﹣1，
每項含有的項數為：1，2，3，…，n，
總共的項數為N=1+2+3+…+n= ，
所有項數的和為Sn：21﹣1+22﹣1+23﹣1+…+2n﹣1=（21+22+23+…+2n）﹣n= ﹣n=2n+1﹣2﹣n，
由題意可知：2n+1為2的整數冪．只需將﹣2﹣n消去即可，
則①1+2+（﹣2﹣n）=0，解得：n=1，總共有 +2=2，不滿足N＞100，
②1+2+4+（﹣2﹣n）=0，解得：n=5，總共有 +3=17，不滿足N＞100，
③1+2+4+8+（﹣2﹣n）=0，解得：n=13，總共有 +4=95，不滿足N＞100，
④1+2+4+8+16（﹣2﹣n）=0，解得：n=29，總共有 +5=440，滿足N＞100，
∴該款軟件的激活碼440．
故選A．
【考點精析】通過靈活運用數列的前n項和，掌握數列{an}的前n項和sn與通項an的關系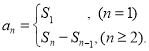即可以解答此題．