【題目】將正整數(shù)12分解成兩個正整數(shù)的乘積有
，
，
三種，其中是這三種分解中，兩數(shù)差的絕對值最小的，我們稱為12的最佳分解．當
是正整數(shù)
的最佳分解時，我們規(guī)定函數(shù)
，例如
.關(guān)于函數(shù)
有下列敘述：①
，②
，③
，④
.其中正確的序號為 （填入所有正確的序號）．
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐
的一個側(cè)面
為等邊三角形，且平面
平面
，四邊形是平行四邊形，
，
，
.
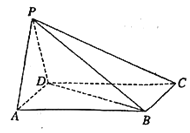
（1）求證：
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，
，點
在橢圓
上．
（
）求橢圓的標準方程．
（
）是否存在斜率為的直線
，使得當直線與橢圓有兩個不同交點
，
時，能在直線
上找到一點
，在橢圓上找到一點
，滿足
？若存在，求出直線的方程；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知以M為圓心的圓M: 
及其上一點A（2，4）
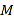
（1）設(shè)圓N與x軸相切，與圓M外切，且圓心N在直線x=6上，求圓N的標準方程；
（2）設(shè)平行于OA的直線l與圓M相交于B、C兩點，且BC=OA,求直線l的方程；
（3）設(shè)點T（t,o）滿足：存在圓M上的兩點P和Q,使得
,求實數(shù)t的取值范圍。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）當
時，求
在區(qū)間
上的最值；
（2）討論函數(shù)的單調(diào)性；
（3）當
時，有
恒成立，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
的前
項和為
，
且滿足:
(1)證明：是等比數(shù)列，并求數(shù)列的通項公式.
(2)設(shè)
，若數(shù)列
是等差數(shù)列，求實數(shù)
的值；
(3)在(2)的條件下，設(shè)
記數(shù)列
的前項和為
，若對任意的
存在實數(shù)
,使得
,求實數(shù)的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（
為自然對數(shù)的底數(shù)）.
(1)求函數(shù)
的極值；
(2)問：是否存在實數(shù)
,使得有兩個相異零點？若存在,求出的取值范圍；若不存在,請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知定義域為
的奇函數(shù)
，滿足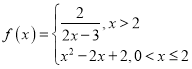
,下面四個關(guān)于函數(shù)的說法：①存在實數(shù)
，使關(guān)于
的方程
有
個不相等的實數(shù)根；②當
時，恒有
；③若當
時，的最小值為
，則
；④若關(guān)于的方程
和
的所有實數(shù)根之和為零，則
．其中說法正確的有______．（將所有正確說法的標號填在橫線上）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某數(shù)學(xué)小組到進行社會實踐調(diào)查，了解到某公司為了實現(xiàn)1000萬元利潤目標，準備制定激勵銷售人員的獎勵方案：在銷售利潤超過10萬元時，按銷售利潤進行獎勵，且獎金y（單位：萬元）隨銷售利潤x（單位：萬元）的增加而增加，但獎金總數(shù)不超過5萬元，同時獎金不超過利潤的25%．同學(xué)們利用函數(shù)知識，設(shè)計了如下的函數(shù)模型，其中符合公司要求的是（參考數(shù)據(jù)：
，
）( )
A.
B.
C.
D.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
