
【題目】已知函數(shù)g![]() =
=![]() -
-![]() sinxcosx-
sinxcosx-![]() sin2x,將其圖象向左移
sin2x,將其圖象向左移![]() 個單位,并向上移
個單位,并向上移![]() 個單位,得到函數(shù)f
個單位,得到函數(shù)f![]() =acos2
=acos2![]() +b
+b![]() 的圖象.
的圖象.
(Ⅰ)求實數(shù)a,b, ![]() 的值;
的值; ![]()
(Ⅱ)設(shè)函數(shù)φ![]() =g
=g![]() -
-![]() f
f![]() ,x∈
,x∈![]() ,求函數(shù)φ
,求函數(shù)φ![]() 的單調(diào)遞增區(qū)間和最值.
的單調(diào)遞增區(qū)間和最值.
【答案】(1) a=1,b=0,φ=![]() ,(2) 單調(diào)增區(qū)間為
,(2) 單調(diào)增區(qū)間為![]() , φ
, φ![]() 的最小值為-
的最小值為-![]() ,最大值為1-
,最大值為1-![]()
【解析】 試題分析:(Ⅰ)利用二倍角的三角函數(shù)以及兩角和的正弦函數(shù),通過函數(shù)的圖象變換,利用變換后的是的表達(dá)式,即可求實數(shù)![]() ,
, ![]() ,
, ![]() 的值;(Ⅱ)求出函數(shù)
的值;(Ⅱ)求出函數(shù)![]() ,
, ![]() 的表達(dá)式,利用正弦函數(shù)的單調(diào)增區(qū)間求出函數(shù)的單調(diào)增區(qū)間,通過增區(qū)間求解函數(shù)的最值.
的表達(dá)式,利用正弦函數(shù)的單調(diào)增區(qū)間求出函數(shù)的單調(diào)增區(qū)間,通過增區(qū)間求解函數(shù)的最值.
試題解析:(Ⅰ)依題意化簡得![]() ,平移
,平移![]() 得
得![]()
∴![]() ,
, ![]() ,
, ![]()
(Ⅱ) ![]()
由![]() 得
得![]()
∵![]()
∴當(dāng)![]() 時,在
時,在![]() 上單調(diào)遞增
上單調(diào)遞增
∴![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ,值域為
,值域為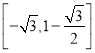
∴![]() 的最小值為
的最小值為![]() ,最大值為
,最大值為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱錐P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中點.

(Ⅰ)求證:PC∥平面EBD;
(Ⅱ)求證:平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(導(dǎo)學(xué)號:05856284)
在△ABC中,角A,B,C的對邊分別為a,b,c,已知c=b(1+2cosA).
(Ⅰ)求證:A=2B;
(Ⅱ)若a=![]() ,B=
,B=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某省高考改革實施方案指出:該省高考考生總成績將由語文、數(shù)學(xué)、外語3門統(tǒng)一高考成績和學(xué)生自主選擇的學(xué)業(yè)水平等級性考試科目共同構(gòu)成.該省教育廳為了解正就讀高中的學(xué)生家長對高考改革方案所持的贊成態(tài)度,隨機從中抽取了100名城鄉(xiāng)家長作為樣本進行調(diào)查,調(diào)查結(jié)果顯示樣本中有25人持不贊成意見.下面是根據(jù)樣本的調(diào)查結(jié)果繪制的等高條形圖.
(1)根據(jù)已知條件與等高條形圖完成下面的2×2列聯(lián)表,并判斷我們能否有95%的把握認(rèn)為“贊成高考改革方案與城鄉(xiāng)戶口有關(guān)”?
贊成 | 不贊成 | 合計 | |||||
城鎮(zhèn)居民 | |||||||
農(nóng)村居民 | |||||||
合計 | |||||||
P(K2≥k0) | 0.10 | 0.05 | 0.005 | ||||
k0 | 2.706 | 3.841 | 7.879 | ||||
注:  其中
其中![]()
(2)用樣本的頻率估計概率,若隨機在全省不贊成高考改革的家長中抽取3個,記這3個家長中是城鎮(zhèn)戶口的人數(shù)為x,試求x的分布列及數(shù)學(xué)期望E(x).

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】【2018屆江蘇省泰州中學(xué)高三12月月考】已知橢圓的中心為坐標(biāo)原點![]() ,橢圓短軸長為
,橢圓短軸長為![]() ,動點
,動點![]() (
(![]() )在橢圓的準(zhǔn)線上.
)在橢圓的準(zhǔn)線上.
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)求以![]() 為直徑且被直線
為直徑且被直線![]() 截得的弦長為
截得的弦長為![]() 的圓的方程;
的圓的方程;
(3)設(shè)![]() 是橢圓的右焦點,過點
是橢圓的右焦點,過點![]() 作
作![]() 的垂線與以
的垂線與以![]() 為直徑的圓交于點
為直徑的圓交于點![]() ,求證:線段
,求證:線段![]() 的長為定值,并求出這個定值.
的長為定值,并求出這個定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}是等比數(shù)列,首項a1=1,公比q>0,其前n項和為Sn,且S1+a1,S3+a3,S2+a2成等差數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)若數(shù)列{bn}滿足an+1=![]() ,Tn為數(shù)列{bn}的前n項和,若Tn≥m恒成立,求m的最大值.
,Tn為數(shù)列{bn}的前n項和,若Tn≥m恒成立,求m的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(導(dǎo)學(xué)號:05856321)已知函數(shù)f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分圖象如圖所示,若A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),則函數(shù)f(x)的單調(diào)增區(qū)間為( )
),則函數(shù)f(x)的單調(diào)增區(qū)間為( )

A. [-![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z) B. [
+2kπ](k∈Z) B. [![]() +2kπ,
+2kπ, ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
C. [-![]() +kπ,
+kπ, ![]() +kπ](k∈Z) D. [
+kπ](k∈Z) D. [![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
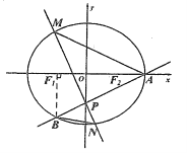
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() ,與橢圓交于另一個點
,與橢圓交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點(
兩點(![]() 不與
不與![]() 重合),若
重合),若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com