
【題目】過拋物線![]() :
:![]() 的焦點
的焦點![]() 的直線
的直線![]() (傾斜角為銳角)交拋物線于
(傾斜角為銳角)交拋物線于![]() ,
,![]() 兩點,若
兩點,若![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() 并延長交拋物線
并延長交拋物線![]() 于點
于點![]() ,已知
,已知![]() ,則直線
,則直線![]() 的斜率是( )
的斜率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中數學 來源: 題型:
【題目】如圖是某手機商城2018年華為、蘋果、三星三種品牌的手機各季度銷量的百分比堆積圖(如:第三季度華為銷量約占50%,蘋果銷量約占20%,三星銷量約占30%).根據該圖,以下結論中一定正確的是( )

A.華為的全年銷量最大B.蘋果第二季度的銷量大于第三季度的銷量
C.華為銷量最大的是第四季度D.三星銷量最小的是第四季度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系,將曲線![]() 上的每一個點的橫坐標保持不變,縱坐標縮短為原來的
上的每一個點的橫坐標保持不變,縱坐標縮短為原來的![]() ,得到曲線
,得到曲線![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,
軸的正半軸為極軸,建立極坐標系, ![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的參數方程;
的參數方程;
(Ⅱ)過原點![]() 且關于
且關于![]() 軸對稱的兩條直線
軸對稱的兩條直線![]() 與
與![]() 分別交曲線
分別交曲線![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且點
,且點![]() 在第一象限,當四邊形
在第一象限,當四邊形![]() 的周長最大時,求直線
的周長最大時,求直線![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名射擊運動員進行射擊比賽,甲的中靶概率為0.8,乙的中靶概率為0.9,求下列事件的概率:
(1)兩人都中靶;
(2)恰好有一人中靶;
(3)兩人都脫靶;
(4)至少有一人中靶.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人獨立地解決同一問題,甲解出此問題的概率是![]() ,乙解出此問題的概率是
,乙解出此問題的概率是![]() .求:
.求:
(1)甲、乙都解出此問題的概率;
(2)甲、乙都未解出此問題的概率;
(3)甲、乙恰有一人解出此問題的概率;
(4)至少有一人解出此問題的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】質檢部門從某超市銷售的甲、乙兩種食用油中分別隨機抽取100桶檢測某項質量指標,由檢測結果得到如圖的頻率分布直方圖:
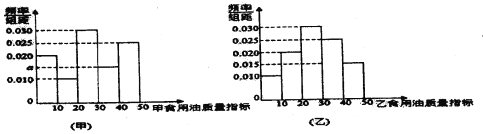
(I)寫出頻率分布直方圖(甲)中![]() 的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為
的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為![]() ,試比較
,試比較![]() 的大小(只要求寫出答案);
的大小(只要求寫出答案);
(Ⅱ)佑計在甲、乙兩種食用油中各隨機抽取1桶,恰有一個桶的質量指標大于20,且另—個桶的質量指標不大于20的概率;
(Ⅲ)由頻率分布直方圖可以認為,乙種食用油的質量指標值![]() 服從正態分布
服從正態分布![]() .其中
.其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,設
,設![]() 表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55, 38.45)的桶數,求
表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55, 38.45)的桶數,求![]() 的數學期望.
的數學期望.
注:①同一組數據用該區間的中點值作代表,計算得![]() :
:
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com