
【題目】設(shè)函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若存在![]() 、
、![]() 滿足
滿足![]() .求證:
.求證: ![]() (其中
(其中![]() 為
為![]() 的導函數(shù))
的導函數(shù))
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)f′(x)=![]() ,(x>0).對a分類討論:a≤0,a>0,即可得出單調(diào)性;(2)不妨設(shè)
,(x>0).對a分類討論:a≤0,a>0,即可得出單調(diào)性;(2)不妨設(shè)![]() ,于是
,于是![]()
![]() ,可得
,可得![]() .當
.當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
故只要證![]() 即可,即證明
即可,即證明![]()
![]() ,即證
,即證![]() .設(shè)
.設(shè)![]() .令
.令![]() ,利用導數(shù)研究其單調(diào)性即可證明結(jié)論.
,利用導數(shù)研究其單調(diào)性即可證明結(jié)論.
試題解析:
(1)由題知![]()
![]()
![]() .
.
當![]() ,此時函數(shù)
,此時函數(shù)![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
當![]() ,此時函數(shù)
,此時函數(shù)![]() 在
在![]() 單調(diào)遞增.
單調(diào)遞增.
(2)因為![]() ,由(1)知
,由(1)知![]()
不妨設(shè)![]() ,由
,由![]() 得,
得, ![]()
![]()
即![]() ,
,
![]()
![]()
![]()
所以![]() .
.
又因為當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
故只要證![]() ,又
,又![]() ,只要證
,只要證![]()
即證明![]()
![]() ,
,
即證![]() ,
,
也就是證![]() .
.
設(shè)![]() .令
.令![]() ,則
,則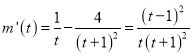 .
.
因為![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上是增函數(shù).
上是增函數(shù).
又![]() ,所以當
,所以當![]() ,
, ![]() 總成立,
總成立,
原題得證.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:高中數(shù)學 來源: 題型:
【題目】近年來隨著我國在教育利研上的投入不斷加大,科學技術(shù)得到迅猛發(fā)展,國內(nèi)企業(yè)的國際競爭力得到大幅提升.伴隨著國內(nèi)市場增速放緩,國內(nèi)確實力企業(yè)紛紛進行海外布局,第二輪企業(yè)出海潮到來,如在智能手機行業(yè),國產(chǎn)品牌已在趕超國外巨頭,某品牌手機公司一直默默拓展海外市場,在海外共設(shè)30多個分支機構(gòu),需要國內(nèi)公司外派大量70后、80后中青年員工.該企業(yè)為了解這兩個年齡層員工是否愿意被外派上作的態(tài)度,按分層抽樣的方式從70后利80后的員工中隨機調(diào)查了100位,得到數(shù)據(jù)如下表:
愿意被外派 | 不愿意被外派 | 合計 | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合計 | 60 | 40 | 100 |
(1)根據(jù)凋查的數(shù)據(jù),是否有![]() 的把握認為“是否愿意被外派與年齡有關(guān)”,并說明理由;
的把握認為“是否愿意被外派與年齡有關(guān)”,并說明理由;
(2)該公司參觀駐海外分支機構(gòu)的交流體驗活動,擬安排4名參與調(diào)查的70后員工參加,70后的員工中有愿意被外派的3人和不愿意被外派的3人報名參加,現(xiàn)采用隨機抽樣方法從報名的員工中選4人,求選到愿意被外派人數(shù)不少于不愿意被外派人數(shù)的概率.
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(參考公式: 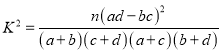 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 經(jīng)過
經(jīng)過![]() 的右頂點和上頂點.
的右頂點和上頂點.
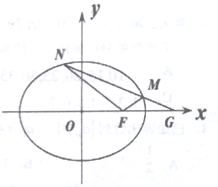
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 作斜率不為
作斜率不為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,求
兩點,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
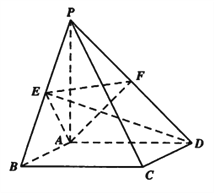
【題目】在四棱錐![]() 中,底面
中,底面![]() 是矩形,側(cè)棱
是矩形,側(cè)棱![]() 底面
底面![]() ,
, ![]() 分別是
分別是![]() 的中點,
的中點, ![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證: ![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,求三棱錐
,求三棱錐![]() 的體積..
的體積..
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
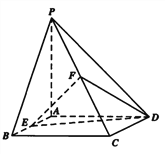
【題目】在四棱錐![]() 中,底面
中,底面![]() 是矩形,側(cè)棱
是矩形,側(cè)棱![]() 底面
底面![]() ,
, ![]() 分別是
分別是![]() 的中點,
的中點, ![]() ,
, ![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等差數(shù)列{an}中,a2=5,S5=40.等比數(shù)列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通項公式
(2)令cn=anbn,求數(shù)列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為拉動經(jīng)濟增長,某市決定新建一批重點工程,分別為基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程三類,這三類工程所含項目的個數(shù)分別占總數(shù)的![]() .現(xiàn)有3名工人獨立地從中任選一個項目參與建設(shè).
.現(xiàn)有3名工人獨立地從中任選一個項目參與建設(shè).
(1)求他們選擇的項目所屬類別互不相同的概率;
(2)記ξ為3人中選擇的項目屬于基礎(chǔ)設(shè)施工程或產(chǎn)業(yè)建設(shè)工程的人數(shù),求ξ的分布列及均值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在極坐標系中曲線![]() 的方程是
的方程是![]() ,點
,點![]() 是
是![]() 上的動點,點
上的動點,點![]() 滿足
滿足![]() (
(![]() 為極點),點
為極點),點![]() 的軌跡為曲線
的軌跡為曲線![]() ,以極點
,以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系
軸的非負半軸建立平面直角坐標系![]() ,已知直線
,已知直線![]() 的參數(shù)方程是
的參數(shù)方程是![]() ,(
,( ![]() 為參數(shù)).
為參數(shù)).
(Ⅰ)求曲線![]() 直角坐標方程與直線
直角坐標方程與直線![]() 的普通方程;
的普通方程;
(Ⅱ)求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知△ABC的內(nèi)角A, B, C的對邊分別為a, b, c,且![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)設(shè)角A的平分線交BC于D,且AD=![]() ,若b=
,若b=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com