
【題目】數列
(1)在等差數列{an}中,a6=10,S5=5,求該數列的第8項a8;
(2)在等比數列{bn}中,b1+b3=10,b4+b6= ![]() ,求該數列的前5項和S5 .
,求該數列的前5項和S5 .
【答案】
(1)解:設數列{an}的公差為d,由已知a6=10,S5=5,
得 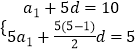 ,
,
解得 ![]() ,
,
所以a8=a1+7d=﹣5+7×3=16.
(或者a8=a6+2d=10+2×3=16)
(2)解:解法一:設數列{bn}的公比為q,由已知 ![]() ,
,
得 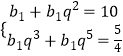 ,
,
解得 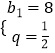 ,
,
所以 ![]() =
= 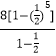 =
= ![]() .
.
解法二:設數列{bn}的公比為q.
由 ![]() ,得
,得 ![]() ,
,
從而得 ![]() .
.
又因為 ![]() ,
,
從而得b1=8.(9分)
所以 ![]() =
= 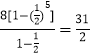 .
.
【解析】(1)由等差數列通項公式列出方程組,求出首項與公差,由此能求出該數列的第8項a8 . (2)法一:由等比數列通項公式列出方程組,求出首項與公比,由此能求出該數列的前5項和S5;法二:由 ![]() ,得
,得 ![]() ,從而求出公比,進而得b1 , 由此能求出該數列的前5項和S5 .
,從而求出公比,進而得b1 , 由此能求出該數列的前5項和S5 .
【考點精析】通過靈活運用等差數列的通項公式(及其變式)和等比數列的前n項和公式,掌握通項公式:![]() 或
或![]() ;前
;前![]() 項和公式:
項和公式: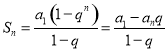 即可以解答此題.
即可以解答此題.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中點,E,F分別為PD,PC的中點.
(Ⅰ)求證:AE⊥平面PCD;
(Ⅱ)求二面角B﹣PA﹣C的余弦值;
(Ⅲ)在棱PB上是否存在點M,使得CM∥平面AEF?若存在,求 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Sn表示數列{an}的前n項和,若對任意的n∈N*滿足an+1=an+a2 , 且a3=2,則S2016=( )
A.1006×2013
B.1006×2014
C.1008×2015
D.1007×2015
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某飛行器在4千米高空飛行,從距著陸點A的水平距離10千米處開始下降,已知下降飛行軌跡為某三次函數圖象的一部分,則該函數的解析式為( ) 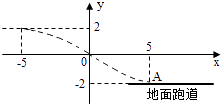
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,當x≥0時,f(x)=x2﹣2x﹣1.
(1)求f(x)的函數解析式,并用分段函數的形式給出;
(2)作出函數f(x)的簡圖;
(3)寫出函數f(x)的單調區間及最值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C的參數方程 ![]() (φ為參數),以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數),以O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求圓C的極坐標方程;
(2)直線l的極坐標方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射線OM:θ=
,射線OM:θ= ![]() 與圓C的交點為O、P,與直線l的交點為Q,求線段PQ的長.
與圓C的交點為O、P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com