【題目】在△ABC中，角A，B，C的對邊分別為a，b，c，已知 
cosB+ 
cosA= 
（I）求∠C的大小；
（II）求sinB﹣ 
sinA的最小值．
【答案】解：（I）由正弦定理，得 
， 
． 所以， 
，即 
．
∵A+B+C=π，∴sin（A+B）=sinC．
∴2cosC= 
，cosC= 
∵C∈（0，π），∴C= 
．
（ II）∵A+B+C=π∴A+B= 
∴sinB﹣ sinA=sin（ 
）﹣ sinA= 
=cos（A+ 
），
∵A+B= ，∴A 
，∴A+ 
∴cos（A+ ）最小值為﹣1．即sinB﹣ sinA的最小值為﹣1．
【解析】（I）由正弦定理，得 
．即cosC= 
，可得C= 
．（II）sinB﹣ 
sinA=sin（ 
）﹣ sinA 
=cos（A+ 
） 由A+B= 
，cos（A+ ）最小值為﹣1．即可得sinB﹣ sinA的最小值
暑假作業暑假快樂練西安出版社系列答案科目：高中數學 來源： 題型：
【題目】某大學藝術專業400名學生參加某次測評，根據男女學生人數比例，使用分層抽樣的方法從中隨機抽取了100名學生，記錄他們的分數，將數據分成7組：[20,30），[30,40），┄，[80,90]，并整理得到如下頻率分布直方圖：
（Ⅰ）從總體的400名學生中隨機抽取一人，估計其分數小于70的概率；
（Ⅱ）已知樣本中分數小于40的學生有5人，試估計總體中分數在區間[40,50）內的人數；
（Ⅲ）已知樣本中有一半男生的分數不小于70，且樣本中分數不小于70的男女生人數相等．試估計總體中男生和女生人數的比例．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知各項都為正數的數列{an}滿足a1=1，an2﹣（2an﹣1﹣1）an﹣2an﹣1=0（n≥2，n∈N*），數列{bn}滿足b1=1，b1+ 
b2+ 
b3+…+ 
bn=bn+1﹣1（n∈N*）
（Ⅰ）求{an}，{bn}的通項公式；
（Ⅱ）求數列{anbn}的前n項和為Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱
中， 
平面
， 
， 
， 
， 
， 
為
的中點.
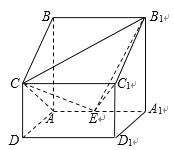
（Ⅰ）求四棱錐
的體積；
（Ⅱ）設點
在線段
上，且直線
與平面
所成角的正弦值為
，求線段
的長度；
（Ⅲ）判斷線段
上是否存在一點
，使得
？（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體，關于其結構特征，下列說法不正確的是
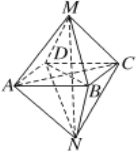
A. 該幾何體是由兩個同底的四棱錐組成的幾何體
B. 該幾何體有12條棱、6個頂點
C. 該幾何體有8個面，并且各面均為三角形
D. 該幾何體有9個面，其中一個面是四邊形，其余均為三角形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
、圓
均滿足圓心在直線
： 
上，過點
，且與直線l2：x=-1相切．
（1）當
時，求圓，圓的標準方程；
（2）直線l2與圓、圓分別相切于A，B兩點，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖為一個纜車示意圖，該纜車半徑為4.8m，圓上最低點與地面距離為0.8m,60秒轉動一圈，圖中OA與地面垂直，以OA為始邊，逆時針轉動θ角到OB，設B點與地面距離是h.
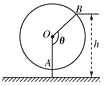
(1)求h與θ間的函數關系式；
(2)設從OA開始轉動，經過t秒后到達OB，求h與t之間的函數關系式，并求纜車到達最高點時用的最少時間是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
