【題目】已知曲線 
（t為參數）， 
（ 
為參數）．
（1）化 
的方程為普通方程；
（2）若 
上的點對應的參數為 
，Q為 
上的動點，求PQ中點M到直線（t為參數）距離的最小值．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某調查機構對本市小學生課業負擔情況進行了調查，設平均每人每天做作業的時間為x分鐘．有1000名小學生參加了此項調查，調查所得數據用程序框圖處理，若輸出的結果是680，則平均每天做作業的時間在0～60分鐘內的學生的頻率是（ ）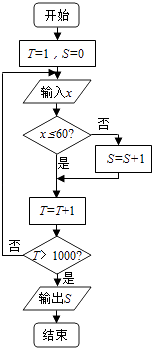 
A.680
B.320
C.0.68
D.0.32
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的三個內角A，B，C所對的邊分別為a，b，c，向量 
， 
，且 
．
（1）求A的大小；
（2）現在給出下列三個條件：①a=1；② 
；③B=45°，試從中選擇兩個條件以確定△ABC，求出所確定的△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為確定下一年度投入某種產品的宣傳費，需了解年宣傳費
（單位：萬元）對年銷售量
（單位：噸）和年利潤
（單位：萬元）的影響。對近六年的年宣傳費
和年銷售量
的數據作了初步統計，得到如下數據：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣傳費 | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量 | 16．8 | 18．8 | 20．7 | 22．4 | 24．0 | 25．5 |
經電腦模擬，發現年宣傳費（萬元）與年銷售量（噸）之間近似滿足關系式
即
。對上述數據作了初步處理，得到相關的值如下表：
|
|
|
|
75．3 | 24．6 | 18．3 | 101．4 |
（1）根據所給數據，求
關于
的回歸方程；
（2）規定當產品的年銷售量
（噸）與年宣傳費
（萬元）的比值在區間
內時認為該年效益良好。現從這6年中任選3年，記其中選到效益良好年的數量為
，試求隨機變量
的分布列和期望。（其中
為自然對數的底數， 
）
附：對于一組數據
，其回歸直線
中的斜率和截距的最小二乘估計分別為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】二次函數f（x）=ax2+bx+c（a，b∈R，a≠0）滿足條件：
①當x∈R時，f（x）的圖象關于直線x=﹣1對稱；②f（1）=1；③f（x）在R上的最小值為0；
（1）求函數f（x）的解析式；
（2）求最大的m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤x．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，幾何體是圓柱的一部分，它是由矩形
（及其內部）以
邊所在直線為旋轉軸旋轉
得到的， 
是
的中點.
（
）設
是
上的一點，且
，求
的大小;
（
）當
時,求二面角
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
