
【題目】已知曲線 ![]() (t為參數),
(t為參數), ![]() (θ為參數),
(θ為參數),
(1)化C1 , C2的方程為普通方程,并說明它們分別表示什么曲線;
(2)若C1上的點P對應的參數為 ![]() ,Q為C2上的動點,求PQ中點M到直線
,Q為C2上的動點,求PQ中點M到直線 ![]() (t為參數)距離的最小值.
(t為參數)距離的最小值.
【答案】
(1)解:∵曲線 ![]() (t為參數),利用同角三角函數的基本關系消去參數t,化為普通方程 (x+4)2+(y﹣3)2=1,
(t為參數),利用同角三角函數的基本關系消去參數t,化為普通方程 (x+4)2+(y﹣3)2=1,
表示以(﹣4,3)為圓心,以1為半徑的圓.
∵ ![]() (θ為參數),利用同角三角函數的基本關系消去參數t,化為普通方程為
(θ為參數),利用同角三角函數的基本關系消去參數t,化為普通方程為 ![]() +
+ ![]() =1,
=1,
表示焦點在x軸上的一個橢圓
(2)解:C1上的點P對應的參數為 ![]() ,Q為C2上的動點,可得點p(﹣4,4),設Q(8cosθ,3sinθ),則 PQ中點M(4cosθ﹣2,
,Q為C2上的動點,可得點p(﹣4,4),設Q(8cosθ,3sinθ),則 PQ中點M(4cosθ﹣2, ![]() ).
).
直線C3 即 x﹣2y﹣7=0.故PQ中點M到直線C3:x﹣2y﹣7=0 的距離為 ![]() =
= ![]()
= ![]() ≥
≥ ![]() =
= ![]() .
.
故PQ中點M到直線 ![]() (t為參數)距離的最小值為
(t為參數)距離的最小值為 ![]()
【解析】(1)把參數方程利用同角三角函數的基本關系消去參數,化為普通方程,從而得到它們分別表示什么曲線.(2)求出點p(﹣4,4),設Q(8cosθ,3sinθ),則 PQ中點M(4cosθ﹣2, ![]() ).利用點到直線的距離公式求出PQ中點M到直線
).利用點到直線的距離公式求出PQ中點M到直線 ![]() (t為參數)距離 為
(t為參數)距離 為 ![]() ,再由正弦函數的值域求得它的最小值.
,再由正弦函數的值域求得它的最小值.
【考點精析】解答此題的關鍵在于理解直線的參數方程的相關知識,掌握經過點![]() ,傾斜角為
,傾斜角為![]() 的直線
的直線![]() 的參數方程可表示為
的參數方程可表示為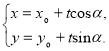 (
(![]() 為參數),以及對圓的參數方程的理解,了解圓
為參數),以及對圓的參數方程的理解,了解圓![]() 的參數方程可表示為
的參數方程可表示為![]() .
.


科目:高中數學 來源: 題型:
【題目】某公司研發出一款產品,批量生產前先在某城市銷售30天進行市場調查.調查結果發現:日銷量![]() 與天數
與天數![]() 的對應關系服從圖①所示的函數關系:每件產品的銷售利潤
的對應關系服從圖①所示的函數關系:每件產品的銷售利潤![]() 與天數
與天數![]() 的對應關系服從圖②所示的函數關系.圖①由拋物線的一部分(
的對應關系服從圖②所示的函數關系.圖①由拋物線的一部分(![]() 為拋物線頂點)和線段
為拋物線頂點)和線段![]() 組成.
組成.
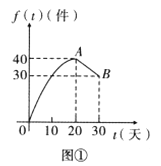
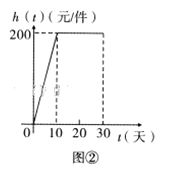
(Ⅰ)設該產品的日銷售利潤![]()
![]() ,分別求出
,分別求出![]() ,
, ![]() ,
, ![]() 的解析式,
的解析式,
(Ⅱ)若在30天的銷售中,日銷售利潤至少有一天超過8500元,則可以投入批量生產,該產品是否可以投入批量生產,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求函數![]() 的單調增區間;
的單調增區間;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再向上平移1個單位,得到函數
個單位,再向上平移1個單位,得到函數![]() 的圖象,若
的圖象,若![]() 在
在![]() 上至少含有10個零點,求
上至少含有10個零點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′(
x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′( ![]() )的值( )
)的值( )
A.必為正數
B.必為負數
C.必為非負
D.必為非正
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線
軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(2)若曲線![]() 上的所有點都在直線
上的所有點都在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來隨著我國在教育科研上的投入不斷加大,科學技術得到迅猛發展,國內企業的國際競爭力得到大幅提升.伴隨著國內市場增速放緩,國內有實力企業紛紛進行海外布局,第二輪企業出海潮到來.如在智能手機行業,國產品牌已在趕超國外巨頭,某品牌手機公司一直默默拓展海外市場,在海外共設![]() 多個分支機構,需要國內公司外派大量
多個分支機構,需要國內公司外派大量![]() 后、
后、![]() 后中青年員工.該企業為了解這兩個年齡層員工是否愿意被外派工作的態度,按分層抽樣的方式從
后中青年員工.該企業為了解這兩個年齡層員工是否愿意被外派工作的態度,按分層抽樣的方式從![]() 后和
后和![]() 后的員工中隨機調查了
后的員工中隨機調查了![]() 位,得到數據如下表:
位,得到數據如下表:
愿意被外派 | 不愿意被外派 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(Ⅰ)根據調查的數據,是否有![]() 以上的把握認為“是否愿意被外派與年齡有關”,并說明理由;
以上的把握認為“是否愿意被外派與年齡有關”,并說明理由;
(Ⅱ)該公司舉行參觀駐海外分支機構的交流體驗活動,擬安排![]() 名參與調查的
名參與調查的![]() 后、
后、![]() 后員工參加.
后員工參加.![]() 后員工中有愿意被外派的
后員工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人報名參加,從中隨機選出
人報名參加,從中隨機選出![]() 人,記選到愿意被外派的人數為
人,記選到愿意被外派的人數為![]() ;
;![]() 后員工中有愿意被外派的
后員工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人報名參加,從中隨機選出
人報名參加,從中隨機選出![]() 人,記選到愿意被外派的人數為
人,記選到愿意被外派的人數為![]() ,求
,求![]() 的概率.
的概率.
參考數據:
|
|
|
|
|
| |
|
|
|
|
|
|
|
(參考公式:![]() ,其中
,其中![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com