
【題目】已知函數f(x)=ex+e-x,g(x)=2x+ax3,a為實常數.
(1)求g(x)的單調區間;
(2)當a=-1時,證明:存在x0∈(0,1),使得y=f(x)和y=g(x)的圖象在x=x0處的切線互相平行.
【答案】(1)見解析;(2)證明見解析.
【解析】
(1)求出函數的導數,通過討論a的范圍,求出函數的單調區間即可;
(2)代入a的值,令h(x)=f′(x)﹣g′(x)=ex﹣e﹣x﹣2+3x2,根據函數的單調性證明即可.
(1)g′(x)=3ax2+2,
當a≥0時,g′(x)>0故g(x)的單調增區間為(﹣∞,+∞).
當a<0時,令g′(x)≥0得![]() x
x![]() ,g(x)的單調增區間為[
,g(x)的單調增區間為[![]() x
x![]() ],
],
g(x)的單調減區間為:(﹣∞,![]() ),(
),(![]() ,+∞)
,+∞)
(2)當a=﹣1時,f′(x)=ex﹣e﹣x,g′(x)=2﹣3x2,
x0∈(0,1),使得y=f(x)和y=g(x)的圖象在x=x0處的切線互相平行.
即x0∈(0,1)使得f′(x0)=g′(x0),且f(x0)≠g(x0),
令h(x)=f′(x)﹣g′(x)=ex﹣e﹣x﹣2+3x2,
h(0)=﹣2<0,h(1)=e![]() 2+3>0,
2+3>0,
∴x0∈(0,1)使得f′(x0)=g′(x0).
∵當x∈(0,![]() )時,g′(x)>0,當x∈(
)時,g′(x)>0,當x∈(![]() ,1)時g′(x)<0,
,1)時g′(x)<0,
∴所以g(x)在區間(0,1)的最大值為g(![]() ),g(
),g(![]() )
)![]() 2.
2.
而f(x)=ex+e﹣x≥2![]() 2,
2,
∴x∈(0,1)時f(x)>g(x)恒成立,∴f(x0)≠g(x0).
從而當a=﹣1時,:x0∈(0,1),使得y=f(x)和y=g(x)的圖象在x=x0處的切線互相平行.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
【題目】近期,某公交公司分別推出支付寶和徽信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,用x表示活動推出的天數,y表示每天使用掃碼支付的人次(單位:十人次),統計數據如表l所示:
表1

根據以上數據,繪制了如右圖所示的散點圖.
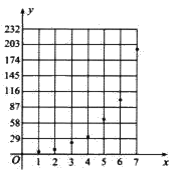
(1)根據散點圖判斷,在推廣期內,![]() (c,d均為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由);
(c,d均為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表1中的數據,求y關于x的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
參考數據:

其中![]()
參考公式:
對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: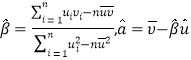 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點
,以極點為原點![]() ,極軸為
,極軸為![]() 軸正半軸(兩坐標系取相同的單位長度)的直角坐標系
軸正半軸(兩坐標系取相同的單位長度)的直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)將曲線![]() 經過伸縮變換
經過伸縮變換 后得到曲線
后得到曲線![]() ,若
,若![]() ,
, ![]() 分別是曲線
分別是曲線![]() 和曲線
和曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某群體的人均通勤時間,是指單日內該群體中成員從居住地到工作地的平均用時.某地上班族![]() 中的成員僅以自駕或公交方式通勤.分析顯示:當
中的成員僅以自駕或公交方式通勤.分析顯示:當![]() 中
中![]() (
(![]() )的成員自駕時,自駕群體的人均通勤時間為
)的成員自駕時,自駕群體的人均通勤時間為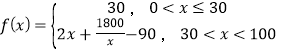 (單位:分鐘),而公交群體的人均通勤時間不受
(單位:分鐘),而公交群體的人均通勤時間不受![]() 影響,恒為
影響,恒為![]() 分鐘,試根據上述分析結果回答下列問題:
分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
(2)求該地上班族![]() 的人均通勤時間
的人均通勤時間![]() 的表達式;討論
的表達式;討論![]() 的單調性,并說明其實際意義.
的單調性,并說明其實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地三角工廠分別位于邊長為2的正方形![]() 的兩個頂點
的兩個頂點![]() 及
及![]() 中點
中點![]() 處.為處理這三角工廠的污水,在該正方形區域內(含邊界)與
處.為處理這三角工廠的污水,在該正方形區域內(含邊界)與![]() 等距的點
等距的點![]() 處建一個污水處理廠,并鋪設三條排污管道
處建一個污水處理廠,并鋪設三條排污管道![]() ,記輔設管道總長為
,記輔設管道總長為![]() 千米.
千米.
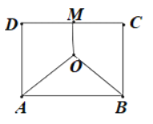
(1)按下列要求建立函數關系式:
(i)設![]() ,將
,將![]() 表示成
表示成![]() 的函數;
的函數;
(ii)設![]() ,將
,將![]() 表示成
表示成![]() 的函數;
的函數;
(2)請你選用一個函數關系,確定污水廠位置,使鋪設管道總長最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】首屆中國國際進口博覽會于2018年11月5日至10日在上海的國家會展中心舉辦.國家展、企業展、經貿論壇、高新產品匯集……首屆進博會高點紛呈.一個更加開放和自信的中國,正用實際行動為世界構筑共同發展平臺,展現推動全球貿易與合作的中國方案.
某跨國公司帶來了高端智能家居產品參展,供購商洽談采購,并決定大量投放中國市場.已知該產品年固定研發成本30萬美元,每生產一臺需另投入90美元.設該公司一年內生產該產品![]() 萬臺且全部售完,每萬臺的銷售收入為
萬臺且全部售完,每萬臺的銷售收入為![]() 萬美元,
萬美元,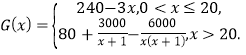
(1)寫出年利潤![]() (萬美元)關于年產量
(萬美元)關于年產量![]() (萬臺)的函數解析式;(利潤=銷售收入-成本)
(萬臺)的函數解析式;(利潤=銷售收入-成本)
(2)當年產量為多少萬臺時,該公司獲得的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)求函數![]() 的極值點;
的極值點;
(2)已知T(![]() ,
,![]() )為函數
)為函數![]() ,
,![]() 的公共點,且函數
的公共點,且函數![]() ,
,![]() 在點T處的切線相同,求a的值;
在點T處的切線相同,求a的值;
(3)若函數![]() 在(0,
在(0,![]() )上的零點個數為2,求a的取值范圍.
)上的零點個數為2,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com