
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 圖象經(jīng)過的定點(diǎn)坐標(biāo);
圖象經(jīng)過的定點(diǎn)坐標(biāo);
(2)當(dāng)![]() 時(shí),求曲線
時(shí),求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程及函數(shù)
處的切線方程及函數(shù)![]() 單調(diào)區(qū)間;
單調(diào)區(qū)間;
(3)若對(duì)任意![]() ,
,![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)見解析(3)
(2)見解析(3)![]() .
.
【解析】
試題分析:(1)當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() ,即可求得頂點(diǎn)坐標(biāo);(2)當(dāng)
,即可求得頂點(diǎn)坐標(biāo);(2)當(dāng)![]() 時(shí),
時(shí),![]() ,對(duì)
,對(duì)![]() 求導(dǎo),分別求出
求導(dǎo),分別求出![]() 與
與![]() ,即可得切線方程,再根據(jù)導(dǎo)函數(shù)的正負(fù),即可求出函數(shù)
,即可得切線方程,再根據(jù)導(dǎo)函數(shù)的正負(fù),即可求出函數(shù)![]() 單調(diào)區(qū)間;(3)對(duì)函數(shù)
單調(diào)區(qū)間;(3)對(duì)函數(shù)![]() 求導(dǎo),討論
求導(dǎo),討論![]() 和
和![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的單調(diào)性,進(jìn)而求出
的單調(diào)性,進(jìn)而求出![]() ,即可求出實(shí)數(shù)
,即可求出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
試題解析:(1)當(dāng)![]() 時(shí),
時(shí),![]()
∴![]() ,
,
∴函數(shù)![]() 的圖象無論
的圖象無論![]() 為何值都經(jīng)過定點(diǎn)
為何值都經(jīng)過定點(diǎn)![]() .
.
(2)當(dāng)![]() 時(shí),
時(shí),![]() .
.
![]() ,
,![]() ,
,![]() ,
,
則切線方程為![]() ,即
,即![]() .
.
在![]() 時(shí),如果
時(shí),如果![]() ,
,
即![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 單調(diào)遞增;
單調(diào)遞增;
如果![]() ,
,
即![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 單調(diào)遞減.
單調(diào)遞減.
(3)![]() ,
,![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
![]() ,
,![]() 不恒成立.
不恒成立.
當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() ,
,![]() .
.
∵![]() 的對(duì)稱軸為
的對(duì)稱軸為![]() ,
,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,且存在唯一
上單調(diào)遞增,且存在唯一![]() ,
,
使得![]() .
.
∴當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,
,![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
∴當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,
,![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴![]() 在
在![]() 上的最大值
上的最大值![]() .
.
∴![]() ,得
,得![]() ,
,
解得![]() .
.


 輕松暑假總復(fù)習(xí)系列答案
輕松暑假總復(fù)習(xí)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班級(jí)體育課舉行了一次“投籃比賽”活動(dòng),為了了解本次投籃比賽學(xué)生總體情況,從中抽取了甲乙兩個(gè)小組樣本分?jǐn)?shù)的莖葉圖如圖所示.
5 | 6 | 5 | 8 | ||||||
6 | 0 | 1 | 3 | 6 | 2 | 4 | 6 | 9 | |
7 | 1 | 2 | 7 | 1 | 3 | ||||
8 | 0 | 1 | 8 | 1 | |||||
甲 | 乙 | ||||||||
(1)分別求甲乙兩個(gè)小組成績的平均數(shù)與方差;
(2)分析比較甲乙兩個(gè)小組的成績;
(3)從甲組高于70分的同學(xué)中,任意抽取2名同學(xué),求恰好有一名同學(xué)的得分在[80,90)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某射擊運(yùn)動(dòng)員每次擊中目標(biāo)的概率都是0.7.現(xiàn)采用隨機(jī)模擬的方法估計(jì)該運(yùn)動(dòng)員射擊4次,至少擊中2次的概率:先由計(jì)算器算出0~9之間取整數(shù)值的隨機(jī)數(shù),指定0,1,2表示沒有擊中目標(biāo),3,4,5,6,7,8,9表示擊中目標(biāo);因?yàn)樯鋼?次,故以每4個(gè)隨機(jī)數(shù)為一組,代表射擊4次的結(jié)果.經(jīng)隨機(jī)模擬產(chǎn)生了20組隨機(jī)數(shù):
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
據(jù)此估計(jì),該射擊運(yùn)動(dòng)員射擊4次至少擊中2次的概率為( )
A. 0.8 B. 0.85 C. 0.9 D. 0.95
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,點(diǎn)P是圓![]() 上一動(dòng)點(diǎn),
上一動(dòng)點(diǎn),![]() x軸于點(diǎn)D.記滿足
x軸于點(diǎn)D.記滿足![]() 的動(dòng)點(diǎn)M的軌跡為Γ.
的動(dòng)點(diǎn)M的軌跡為Γ.
(1)求軌跡Γ的方程;
(2)已知直線![]() 與軌跡Γ交于不同兩點(diǎn)A,B,點(diǎn)G是線段AB中點(diǎn),射線OG交軌跡Γ于點(diǎn)Q,且
與軌跡Γ交于不同兩點(diǎn)A,B,點(diǎn)G是線段AB中點(diǎn),射線OG交軌跡Γ于點(diǎn)Q,且![]() .
.
①證明:![]()
②求△AOB的面積S(λ)的解析式,并計(jì)算S(λ)的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知平面上動(dòng)點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離與到直線
的距離與到直線![]() 的距離之比為
的距離之比為![]() ,記動(dòng)點(diǎn)
,記動(dòng)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設(shè)![]() 是曲線
是曲線![]() 上的動(dòng)點(diǎn),直線
上的動(dòng)點(diǎn),直線![]() 的方程為
的方程為![]() .
.
①設(shè)直線![]() 與圓
與圓![]() 交于不同兩點(diǎn)
交于不同兩點(diǎn)![]() ,
, ![]() ,求
,求![]() 的取值范圍;
的取值范圍;
②求與動(dòng)直線![]() 恒相切的定橢圓
恒相切的定橢圓![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲線
是曲線![]() :
: ![]() 上的動(dòng)點(diǎn),是否存在直線
上的動(dòng)點(diǎn),是否存在直線![]() :
: ![]() 恒相切的定曲線
恒相切的定曲線![]() ?若存在,直接寫出曲線
?若存在,直接寫出曲線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某機(jī)構(gòu)組織語文、數(shù)學(xué)學(xué)科能力競賽,按照一定比例淘汰后,頒發(fā)一二三等獎(jiǎng).現(xiàn)有某考場的兩科考試成績數(shù)據(jù)統(tǒng)計(jì)如下圖所示,其中數(shù)學(xué)科目成績?yōu)槎泉?jiǎng)的考生有![]() 人.
人.
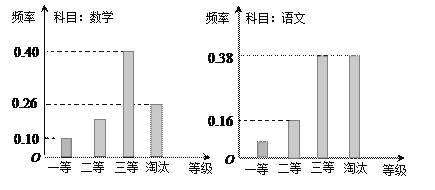

(Ⅰ)求該考場考生中語文成績?yōu)橐坏泉?jiǎng)的人數(shù);
(Ⅱ)用隨機(jī)抽樣的方法從獲得數(shù)學(xué)和語文二等獎(jiǎng)的學(xué)生中各抽取![]() 人,進(jìn)行綜合素質(zhì)測(cè)試,將他們的綜合得分繪成莖葉圖,求樣本的平均數(shù)及方差并進(jìn)行比較分析;
人,進(jìn)行綜合素質(zhì)測(cè)試,將他們的綜合得分繪成莖葉圖,求樣本的平均數(shù)及方差并進(jìn)行比較分析;
(Ⅲ)已知本考場的所有考生中,恰有![]() 人兩科成績均為一等獎(jiǎng),在至少一科成績?yōu)橐坏泉?jiǎng)的考生中,隨機(jī)抽取
人兩科成績均為一等獎(jiǎng),在至少一科成績?yōu)橐坏泉?jiǎng)的考生中,隨機(jī)抽取![]() 人進(jìn)行訪談,求兩人兩科成績均為一等獎(jiǎng)的概率.
人進(jìn)行訪談,求兩人兩科成績均為一等獎(jiǎng)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)判斷函數(shù)的奇偶性,并加以證明;
(2)用定義證明![]() 在
在![]() 上是減函數(shù);
上是減函數(shù);
(3)函數(shù)![]() 在
在![]() 上是單調(diào)增函數(shù)還是單調(diào)減函數(shù)?(直接寫出答案,不要求寫證明過程).
上是單調(diào)增函數(shù)還是單調(diào)減函數(shù)?(直接寫出答案,不要求寫證明過程).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)名著《算法統(tǒng)宗》中有如下問題:“遠(yuǎn)望巍巍塔七層,紅光點(diǎn)點(diǎn)倍加增,共燈三百八十一,請(qǐng)問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數(shù)是上一層燈數(shù)的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com