
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直線l的方程為x=1.
;(2)直線l的方程為x=1.
【解析】試題分析:(1)利用橢圓和拋物線有一個公共焦點和點在橢圓上進行求解;(2) 聯立直線和橢圓的方程,得到關于![]() 的一元二次方程,再利用根與系數的關系、弦長公式和基本不等式進行求解.
的一元二次方程,再利用根與系數的關系、弦長公式和基本不等式進行求解.
試題解析:(1)因為拋物線y2=4![]() x的焦點為(
x的焦點為(![]() ,0),所以橢圓C的半焦距c=
,0),所以橢圓C的半焦距c=![]() ,即a2-b2=3. ①
,即a2-b2=3. ①
把點Q![]() 代入
代入![]() +
+![]() =1,得
=1,得![]() +
+![]() =1. ②
=1. ②
由①②解得a2=4,b2=1.所以橢圓C的標準方程為![]() +y2=1.
+y2=1.
(2)設直線l的方程為x=ty+1,代入![]() +y2=1,
+y2=1,
得(t2+4)y2+2ty-3=0.
設M(x1,y1),N(x2,y2),則有y1+y2=-![]() ,y1y2=-
,y1y2=-![]() .
.
則|y1-y2|=![]() =
=![]() =
=![]() =
=![]() =
=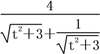 .令
.令![]() =m(m≥
=m(m≥![]() ).易知函數y=m+
).易知函數y=m+![]() 在[
在[![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
則![]() +
+![]() ≥
≥![]() +
+![]() =
=![]() ,當且僅當m=
,當且僅當m=![]() ,即t=0時,取等號.
,即t=0時,取等號.
所以|y1-y2|≤![]() .所以△AMN的面積S=
.所以△AMN的面積S=![]() |AP||y1-y2|≤
|AP||y1-y2|≤![]() ×3×
×3×![]() =
=![]() ,
,
所以Smax=![]() ,此時直線l的方程為x=1.
,此時直線l的方程為x=1.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() 和
和![]() ,離心率是
,離心率是![]() ,直線
,直線![]() 過點
過點![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點,當直線
兩點,當直線![]() 過點
過點![]() 時,
時, ![]() 的周長為
的周長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)當直線![]() 繞點
繞點![]() 運動時,試求
運動時,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直角坐標系中動點![]() ,參數
,參數![]() ,在以原點為極點、
,在以原點為極點、![]() 軸正半軸為極軸所建立的極坐標系中,動點
軸正半軸為極軸所建立的極坐標系中,動點![]() 在曲線
在曲線![]() :
: ![]() 上.
上.
(1)求點![]() 的軌跡
的軌跡![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若動點![]() 的軌跡
的軌跡![]() 和曲線
和曲線![]() 有兩個公共點,求實數
有兩個公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() 為
為![]() 的中點.
的中點.
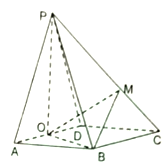
(Ⅰ)若![]() ,求證:平面
,求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,
, ![]() 為等邊三角形,且
為等邊三角形,且![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,底面半徑為![]() ,母線長為
,母線長為![]() 的圓柱的軸截面是四邊形
的圓柱的軸截面是四邊形![]() ,線段
,線段![]() 上的兩動點
上的兩動點![]() ,
, ![]() 滿足
滿足![]() .點
.點![]() 在底面圓
在底面圓![]() 上,且
上,且![]() ,
, ![]() 為線段
為線段![]() 的中點.
的中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱錐![]() 的體積是否為定值,若是,請求出該定值;若不是,請說明理由.
的體積是否為定值,若是,請求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點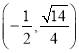 ,且離心率為
,且離心率為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若點![]() 為橢圓
為橢圓![]() 的右頂點,探究:
的右頂點,探究: ![]() 是否為定值,若是,求出該定值,若不是,請說明理由.(其中,
是否為定值,若是,求出該定值,若不是,請說明理由.(其中, ![]() ,
, ![]() 分別是直線
分別是直線![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限接近圓的面積,并創立了“割圓術”,利用“割圓術”,劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”,利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )
(參考數據: ![]() )
)
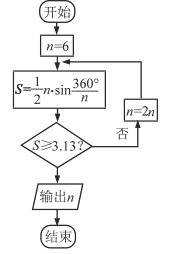
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com