
【題目】在數列{an}中,a1=1,an+1=2an+2n .
(1)設bn= ![]() .證明:數列{bn}是等差數列;
.證明:數列{bn}是等差數列;
(2)求數列{an}的前n項和Sn .
【答案】
(1)解:由an+1=2an+2n.兩邊同除以2n得 ![]()
∴ ![]() ,即bn+1﹣bn=1
,即bn+1﹣bn=1
∴{bn}以1為首項,1為公差的等差數列
(2)解:由(1)得 ![]()
∴an=n2n﹣1
Sn=20+2×21+3×22+…+n2n﹣1
2Sn=21+2×22+…+(n﹣1)2n﹣1+n2n
∴﹣Sn=20+21+22+…+2n﹣1﹣n2n
= ![]()
∴Sn=(n﹣1)2n+1
【解析】(1)由an+1=2an+2n構造可得 ![]() 即數列{bn}為等差數列(2)由(1)可求
即數列{bn}為等差數列(2)由(1)可求 ![]() =n,從而可得an=n2n﹣1 利用錯位相減求數列{an}的和
=n,從而可得an=n2n﹣1 利用錯位相減求數列{an}的和
【考點精析】解答此題的關鍵在于理解等差關系的確定的相關知識,掌握如果一個數列從第2項起,每一項與它的前一項的差等于同一個常數,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么這個數列就叫做等差數列,以及對數列的前n項和的理解,了解數列{an}的前n項和sn與通項an的關系
)那么這個數列就叫做等差數列,以及對數列的前n項和的理解,了解數列{an}的前n項和sn與通項an的關系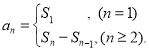 .
.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:
【題目】假設小明訂了一份報紙,送報人可能在早上6:30—7:30之間把報紙送到,小明離家的時間在早上7:00—8:00之間,則他在離開家之前能拿到報紙的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點A(﹣1,2)為圓心的圓與直線m:x+2y+7=0相切,過點B(﹣2,0)的動直線l與圓A相交于M、N兩點
(1)求圓A的方程.
(2)當|MN|=2 ![]() 時,求直線l方程.
時,求直線l方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱臺![]() 中,
中, ![]() 與
與![]() 分別是棱長為1與2的正三角形,平面
分別是棱長為1與2的正三角形,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() 為
為![]() 中點,
中點, ![]() .
.

(Ⅰ)是否存在實數![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅱ)在 (Ⅰ)的條件下,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是正項數列
是正項數列![]() 的前
的前![]() 項和,且
項和,且![]() .
.
(Ⅰ)求數列![]() 通項公式;
通項公式;
(Ⅱ)是否存在等比數列![]() ,使
,使![]() 對一切正整數
對一切正整數![]() 都成立?并證明你的結論.
都成立?并證明你的結論.
(Ⅲ)設![]() (
(![]() ),且數列
),且數列![]() 的前
的前![]() 項和為
項和為![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個說法:
①若函數f(x)=asinx+cosx(x∈R)的圖象關于直線x= ![]() 對稱,則a=
對稱,則a= ![]() ;
;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),若
=(﹣2,m),若 ![]() 與
與 ![]() 的夾角為鈍角,則m<1;
的夾角為鈍角,則m<1;
③當 ![]() <α<
<α< ![]() 時,函數f(x)=sinx﹣logax有三個零點;
時,函數f(x)=sinx﹣logax有三個零點;
④函數f(x)=xsinx在[﹣ ![]() ,0]上單調遞減,在[0,
,0]上單調遞減,在[0, ![]() ]上單調遞增.
]上單調遞增.
其中正確的是(填上所有正確說法的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一枚質地均勻的骰子先后拋擲兩次,若第一次朝上一面的點數為a,第二次朝上一面的點數為b,則函數y=ax2﹣2bx+1在(﹣∞,2]上為減函數的概率是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)
在直角坐標系xOy中,曲線y=x2+mx–2與x軸交于A,B兩點,點C的坐標為(0,1).當m變化時,解答下列問題:
(1)能否出現AC⊥BC的情況?說明理由;
(2)證明過A,B,C三點的圓在y軸上截得的弦長為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com