
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() 是正三角形,
是正三角形,![]() 與
與![]() 的交點為
的交點為![]() ,又
,又![]() ,點
,點![]() 是
是![]() 的中點。
的中點。

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)證明見解析;(2)![]() 。
。
【解析】
試題分析:(1)根據(jù)面面垂直的判定定理先證明![]() 平面
平面![]() ,即可證明平面
,即可證明平面![]() 平面
平面![]() ;(2)建立空間直角坐標(biāo)系,求出平面的法向量,利用利用向量法即可求出二面角
;(2)建立空間直角坐標(biāo)系,求出平面的法向量,利用利用向量法即可求出二面角![]() 的余弦值。
的余弦值。
試題解析:(1)證明:在正三角形![]() 中,
中,![]() ,在
,在![]() 中,∵
中,∵![]() ,易證
,易證![]() ,∴
,∴![]() 為
為![]() 中點,∵點
中點,∵點![]() 是
是![]() 的中點,∴
的中點,∴![]() ,∵
,∵![]() 面
面![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() ,∴平面
,∴平面![]() 。
。
(2)分別以直線![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系,如下圖所示,
軸建立空間直角坐標(biāo)系,如下圖所示,

∴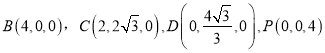 。
。
由(1)可知,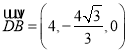 為平面
為平面![]() 的一個法向量,
的一個法向量,![]() ,設(shè)平面
,設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則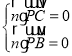 ,即
,即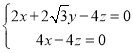 ,令
,令![]() ,解得
,解得![]() ,則平面
,則平面![]() 的一個法向量為
的一個法向量為![]() ,
,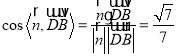 ,由題知二面角
,由題知二面角![]() 為銳二面角,∴二面角
為銳二面角,∴二面角![]() 余弦值為
余弦值為![]() 。
。


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某化工廠引進(jìn)一條先進(jìn)生產(chǎn)線生產(chǎn)某種化工產(chǎn)品,其生產(chǎn)的總成本y(萬元)與年產(chǎn)量x(噸)之間的函數(shù)關(guān)系式可以近視地表示為![]() ,已知此生產(chǎn)線的年產(chǎn)量最大為210噸.
,已知此生產(chǎn)線的年產(chǎn)量最大為210噸.
(1)求年產(chǎn)量為多少噸時,生產(chǎn)每噸產(chǎn)品的平均成本最低,并求最低成本;
(2)若每噸產(chǎn)品平均出廠價為40萬元,那么當(dāng)年產(chǎn)量為多少噸時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某化工廠引進(jìn)一條先進(jìn)生產(chǎn)線生產(chǎn)某種化工產(chǎn)品, 其生產(chǎn)的總成本![]() (萬元)與年產(chǎn)量
(萬元)與年產(chǎn)量![]() (噸)之間的函數(shù)關(guān)系式可以近似地表示為
(噸)之間的函數(shù)關(guān)系式可以近似地表示為![]() ,已知此生產(chǎn)線年產(chǎn)量最大為
,已知此生產(chǎn)線年產(chǎn)量最大為![]() 噸.
噸.
(1)求年產(chǎn)量為多少噸時,生產(chǎn)每噸產(chǎn)品的平均成本最低,并求最低成本;
(2)若毎噸產(chǎn)品平均出廠價為![]() 萬元,那么當(dāng)年產(chǎn)量為多少噸時,可以獲得最大利潤?最大利潤是多少?
萬元,那么當(dāng)年產(chǎn)量為多少噸時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,![]() 是村里一個小湖的一角,其中
是村里一個小湖的一角,其中![]() . 為了給村民營造豐富的休閑環(huán)境,村委會決定在直線湖岸
. 為了給村民營造豐富的休閑環(huán)境,村委會決定在直線湖岸![]() 與
與![]() 上分別建觀光長廊
上分別建觀光長廊![]() 與
與![]() ,其中
,其中![]() 是寬長廊,造價是
是寬長廊,造價是![]() 元/米;
元/米;![]() 是窄長廊,造價是
是窄長廊,造價是![]() 元/米;兩段長廊的總造價預(yù)算為
元/米;兩段長廊的總造價預(yù)算為![]() 萬元(恰好都用完);同時,在線段
萬元(恰好都用完);同時,在線段![]() 上靠近點
上靠近點![]() 的三等分點
的三等分點![]() 處建一個表演舞臺,并建水上通道
處建一個表演舞臺,并建水上通道![]() (表演舞臺的大小忽略不計),水上通道的造價是
(表演舞臺的大小忽略不計),水上通道的造價是![]() 元/米.
元/米.

(1)若規(guī)劃寬長廊![]() 與窄長廊
與窄長廊![]() 的長度相等,則水上通道
的長度相等,則水上通道![]() 的總造價需多少萬元?
的總造價需多少萬元?
(2)如何設(shè)計才能使得水上通道![]() 的總造價最低?最低總造價是多少萬元?
的總造價最低?最低總造價是多少萬元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為常數(shù),且
為常數(shù),且![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)在(1)的條件下,設(shè)函數(shù)![]() ,若
,若![]() 在區(qū)間[-2,2]上是單調(diào)函數(shù),求實數(shù)
在區(qū)間[-2,2]上是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)是否存在實數(shù)![]() 使得函數(shù)
使得函數(shù)![]() 在[-1,4]上的最大值是4?若存在,求出
在[-1,4]上的最大值是4?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(重點班)我們知道對數(shù)函數(shù)![]() ,對任意
,對任意![]() ,都有
,都有![]() 成立,若
成立,若![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() .參照對數(shù)函數(shù)的性質(zhì),研究下題:定義在
.參照對數(shù)函數(shù)的性質(zhì),研究下題:定義在![]() 上的函數(shù)
上的函數(shù)![]() 對任意
對任意![]() ,都有
,都有![]() ,并且當(dāng)且僅當(dāng)
,并且當(dāng)且僅當(dāng)![]() 時,
時,![]() 成立.
成立.
(1)設(shè)![]() ,求證:
,求證:![]() ;
;
(2)設(shè)![]() ,若
,若![]() ,比較
,比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=lgx的圖象為C,作圖象C關(guān)于直線y=x的對稱圖象C1 , 將圖象C1向左平移3個單位后再向下平移兩個單位得到圖象C2 , 若圖象C2所對應(yīng)的函數(shù)為f(x),則f(﹣3)= .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com