
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分別是AC1和BB1的中點,則直線DE與平面BB1C1C所成的角為( )
,D,E分別是AC1和BB1的中點,則直線DE與平面BB1C1C所成的角為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:取AC的中點為F,連接BF、DF. 因為在直三棱柱ABC﹣A1B1C1中,CC1∥BB1 , 又因為DF是三角形ACC1的中位線,故DF= ![]() CC1=
CC1= ![]() BB1=BE,故四邊形BEDF是平行四邊形,所以ED∥BF.
BB1=BE,故四邊形BEDF是平行四邊形,所以ED∥BF.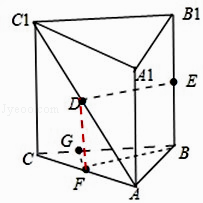
過點F作FG垂直與BC交BC與點G,由題意得∠FBG即為所求的角.
因為AB=1,AC=2,BC= ![]() ,所以∠ABC=
,所以∠ABC= ![]() ,∠BCA=
,∠BCA= ![]() ,直角三角形斜邊中線BF是斜邊AC的一半,故BF=
,直角三角形斜邊中線BF是斜邊AC的一半,故BF= ![]() AC=CF,所以
AC=CF,所以
∠FBG=∠BCA= ![]() .
.
故選A.
根據題意得ED∥BF,進而得到直線DE與平面BB1C1C所成的角等于直線BF與平面BB1C1C所成的角.利用幾何體的結構特征得到∠FBG= ![]() .即可得到答案.
.即可得到答案.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() ,左焦點
,左焦點 ![]() ,且離心率
,且離心率 ![]() (Ⅰ)求橢圓C的方程;
(Ⅰ)求橢圓C的方程;
(Ⅱ)若直線l:y=kx+m(k≠0)與橢圓C交于不同的兩點M,N(M,N不是左、右頂點),且以MN為直徑的圓經過橢圓C的右頂點A.求證:直線l過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于實數x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},則關于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷正確的是 . (填寫所有正確的序號) ①若sinx+siny= ![]() ,則siny﹣cos2x的最大值為
,則siny﹣cos2x的最大值為 ![]() ;
;
②函數y=sin(2x+ ![]() )的單調增區間是[kπ﹣
)的單調增區間是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
③函數f(x)= ![]() 是奇函數;
是奇函數;
④函數y=tan ![]() ﹣
﹣ ![]() 的最小正周期是π.
的最小正周期是π.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2009年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組,得到的頻率分布表如圖所示. 
(1)請先求出頻率分布表中①、②位置相應數據,再在答題紙上完成下列頻率分布直方圖;
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3、4、5組中用分層抽樣抽取6名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試?
(3)在(2)的前提下,學校決定在6名學生中隨機抽取2名學生接受A考官進行面試,求:第4組至少有一名學生被考官A面試的概率?
組號 | 分組 | 頻數 | 頻率 |
第1組 | [160,165) | 5 | 0.050 |
第2組 | [165,170) | ① | 0.350 |
第3組 | [170,175) | 30 | ② |
第4組 | [175,180) | 20 | 0.200 |
第5組 | [180,185) | 10 | 0.100 |
合計 | 100 | 1.00 | |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比數列,公比不為1.
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某實驗室一天的溫度(單位:℃)隨時間t(單位:h)的變化近似滿足函數關系: f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求實驗室這一天的最大溫差;
(Ⅱ)若要求實驗室溫度不高于11℃,則在哪段時間實驗室需要降溫?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題P:實數x滿足2x2﹣5ax﹣3a2<0,其中a>0,命題q:實數x滿足 ![]() .
.
(1)若a=2,且p∧q為真,求實數x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com