
【題目】已知函數 ![]() .
.
(1)用五點作圖法畫出![]() 在長度為一個周期的區間上的圖象;
在長度為一個周期的區間上的圖象;

(2))求函數![]() 的單調遞增區間;
的單調遞增區間;
(3)簡述如何由![]() 的圖象經過適當的圖象變換得到
的圖象經過適當的圖象變換得到![]() 的圖象?
的圖象?
科目:高中數學 來源: 題型:
【題目】已知橢圓系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是橢圓
是橢圓![]() 的焦點,
的焦點, ![]() 是橢圓
是橢圓![]() 上一點,且
上一點,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 為橢圓
為橢圓![]() 上任意一點,過
上任意一點,過![]() 且與橢圓
且與橢圓![]() 相切的直線
相切的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() ,求證:
,求證: ![]() 的面積為定值,并求出這個定值.
的面積為定值,并求出這個定值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,成于公元一世紀左右,系統總結了戰國、秦、漢時期的數學成就.其中《方田》一章中記載了計算弧田(弧田就是由圓弧和其所對弦所圍成弓形)的面積所用的經驗公式:弧田面積=![]() (弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為
(弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為![]() ,弦長為
,弦長為![]() 的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中
的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為慶祝成立二十周年,特舉辦《快樂大闖關》競技類有獎活動,該活動共有四關,由兩名男職員與兩名女職員組成四人小組,設男職員闖過一至四關概率依次是![]() ,女職員闖過一至四關的概率依次是
,女職員闖過一至四關的概率依次是![]()
(1)求女職員闖過四關的概率;
(2)設![]() 表示四人小組闖過四關的人數,求隨機變量
表示四人小組闖過四關的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在十九大“建設美麗中國”的號召下,某省級生態農業示范縣大力實施綠色生產方案,對某種農產品的生產方式分別進行了甲、乙兩種方案的改良。為了檢查甲、乙兩種方案的改良效果,隨機在這兩種方案中各任意抽取了![]() 件產品作為樣本逐件稱出它們的重量(單位:克),重量值落在
件產品作為樣本逐件稱出它們的重量(單位:克),重量值落在![]() 之間的產品為合格品,否則為不合格品。下表是甲、乙兩種方案樣本頻數分布表。
之間的產品為合格品,否則為不合格品。下表是甲、乙兩種方案樣本頻數分布表。
產品重量 | 甲方案頻數 | 乙方案頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求出甲(同組中的重量值用組中點值代替)方案樣本中![]() 件產品的平均數;
件產品的平均數;
(2)若以頻率作為概率,試估計從兩種方案分別任取![]() 件產品,恰好兩件產品都是合格品的概率分別是多少;
件產品,恰好兩件產品都是合格品的概率分別是多少;
(3)由以上統計數據完成下面![]() 列聯表,并回答有多大把握認為“產品是否為合格品與改良方案的選擇有關”.
列聯表,并回答有多大把握認為“產品是否為合格品與改良方案的選擇有關”.
甲方案 | 乙方案 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
參考公式: 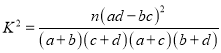 ,其中
,其中![]() .
.
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 是函數
是函數![]() (
(![]() ,
,![]() )圖象上的任意兩點,且角
)圖象上的任意兩點,且角![]() 的終邊經過點
的終邊經過點![]() ,若
,若![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() +
+![]() =1(a>b>0)的焦點分別為F1(0,-1),F2(0,1),且3a2=4b2.
=1(a>b>0)的焦點分別為F1(0,-1),F2(0,1),且3a2=4b2.
(1)求橢圓的方程;
(2)設點P在這個橢圓上,且|PF1|-|PF2|=1,求∠F1PF2的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,F1 , F2分別為橢圓 ![]() +
+ ![]() =1(a>b>0)的左、右焦點,頂點B的坐標為(0,b),連接BF2并延長交橢圓于點A,過點A作x軸的垂線交橢圓于另一點C,連接F1C.
=1(a>b>0)的左、右焦點,頂點B的坐標為(0,b),連接BF2并延長交橢圓于點A,過點A作x軸的垂線交橢圓于另一點C,連接F1C. 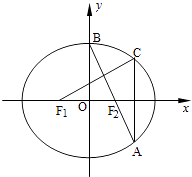
(1)若點C的坐標為( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求橢圓的方程;
,求橢圓的方程;
(2)若F1C⊥AB,求橢圓離心率e的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com