Question

【題目】已知橢圓與直線都經過點.直線與平行，且與橢圓交于兩點，直線與軸分別交于兩點.

（1）求橢圓的方程；

（2）證明： 為等腰三角形.

Answer 1

【答案】(1) ；(2)證明見解析.

【解析】試題分析：（1）將點M分別代入直線方程及橢圓方程，即可求得a和b的值，求得橢圓方程；
（2）設直線m的方程，代入橢圓方程，利用韋達定理及直線的斜率公式求得kMA+kMB=0，即可求得△MEF為等腰三角形．

試題解析：

（1）由直線都經過點，則a=2b，將代入橢圓方程： ，解得：b2=4，a2=16，橢圓的方程為。

（2）設直線為： ，

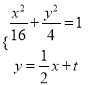聯立: ，得

于是

設直線的斜率為，要證為等腰三角形，只需

，

，

，

，

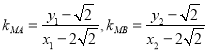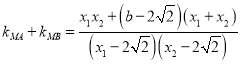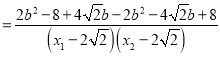所以為等腰三角形.

點睛: 本題考查橢圓的標準方程，直線與橢圓的位置關系，考查韋達定理，直線的斜率公式，考查計算能力，證明三角形為等腰三角形轉化為證明斜率之和為0是關鍵.