
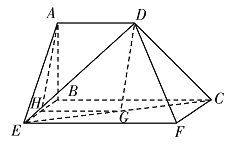
【題目】下面是幾何體![]() 的三視圖及直觀圖.
的三視圖及直觀圖.

(1)試判斷線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,請說明理由;
,請說明理由;
(2)證明:![]() .
.
【答案】(1)見解析;(2)見解析
【解析】分析:(1)取BC與EC的中點H,G,可證HG與AD平行且相等,從而得ADGH是平行四邊形,因此有AH//DG,從而得線面平行;
(2)由題中條件證明垂直后計算出![]() 的長度,再用勾股定理逆定理證得
的長度,再用勾股定理逆定理證得![]() .
.
詳解: (1)存在線段![]() 的中點
的中點![]() ,使得
,使得![]() 平面
平面![]() ,理由如下:
,理由如下:
由三視圖可知,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]()
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
因為![]() 為
為![]() 中點,所以
中點,所以![]()
![]() ,且
,且![]()
因為四邊形![]() 是直角梯形,
是直角梯形,![]() ,且
,且![]() ,
,
所以![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]()
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,因為四邊形
,因為四邊形![]() 為矩形,
為矩形,
所以![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,故
,故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,故
,故![]() ,
,
因為四邊形![]() 為直角梯形,
為直角梯形,![]() ,且
,且![]() ,
,
所以![]() ,∴
,∴![]() .
.
又![]() ,即
,即![]() ,故
,故![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池![]() 的池底水平鋪設污水凈化管道(
的池底水平鋪設污水凈化管道(![]() ,
,![]() 是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口
是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口![]() 是
是![]() 的中點,
的中點,![]() 分別落在線段
分別落在線段![]() 上.已知
上.已知![]() 米,
米,![]() 米,記
米,記![]() .
.
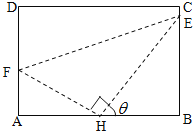
(1)試將污水凈化管道的長度![]() 表示為
表示為![]() 的函數,并寫出定義域;
的函數,并寫出定義域;
(2)若![]() ,求此時管道的長度
,求此時管道的長度![]() ;
;
(3)當![]() 取何值時,污水凈化效果最好?并求出此時管道的長度.
取何值時,污水凈化效果最好?并求出此時管道的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】復利是一種計算利息的方法.即把前一期的利息和本金加在一起算作本金,再計算下一期的利息.某同學有壓歲錢1000元,存入銀行,年利率為2.25%;若放入微信零錢通或
者支付寶的余額寶,年利率可達4.01%.如果將這1000元選擇合適方式存滿5年,可以多獲利息( )元.(參考數據:![]() )
)
A. 176 B. 100 C. 77 D. 88
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為調查高三年學生的身高情況,按隨機抽樣的方法抽取80名學生,得到男生身高情況的頻率分布直方圖(圖(1))和女生身高情況的頻率分布直方圖(圖(2)).已知圖(1)中身高在170~175cm的男生人數有16人.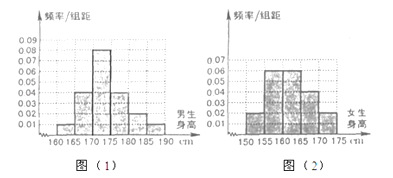
(Ⅰ)試問在抽取的學生中,男、女生各有多少人?
(Ⅱ)根據頻率分布直方圖,完成下列的2×2列聯表,并判斷能有多大(百分幾)的把握認為“身高與性別有關”?
≥170cm | <170cm | 總計 | |
男生身高 | |||
女生身高 | |||
總計 |
(Ⅲ)在上述80名學生中,從身高在170~175cm之間的學生中按男、女性別分層抽樣的方法,抽出5人,從這5人中選派3人當旗手,求3人中恰好有一名女生的概率.
參考公式:K2=![]()
參考數據:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設樣本數據x1 , x2 , …,x10的均值和方差分別為1和4,若yi=xi+a(a為非零常數,i=1,2,…,10),則y1 , y2 , …,y10的均值和方差分別為( )
A.1+a,4
B.1+a,4+a
C.1,4
D.1,4+a
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以原點
為參數).在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
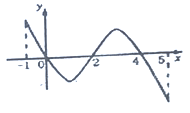
【題目】已知函數![]() 的定義域為
的定義域為![]() ,部分對應值如下表,
,部分對應值如下表,![]() 的導函數
的導函數![]() 的圖象如圖所示,給出關于
的圖象如圖所示,給出關于![]() 的下列命題:
的下列命題:
①函數![]() 在
在![]() 處取得極小值;
處取得極小值;
②函數![]() 在
在![]() 是減函數,在
是減函數,在![]() 是增函數;
是增函數;
③當![]() 時,函數
時,函數![]() 有4個零點;
有4個零點;
④如果當![]() 時,
時,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值為0.
的最小值為0.
其中所有的正確命題是__________(寫出正確命題的序號).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com