【題目】對下列命題：
①直線
與函數(shù)
的圖象相交，則相鄰兩交點的距離為
；
②點
是函數(shù)的圖象的一個對稱中心；
③函數(shù)
在
上單調遞減，則
的取值范圍為
；
④函數(shù)
若
對
R恒成立，則
.
其中所有正確命題的序號為____
新思維假期作業(yè)寒假吉林大學出版社系列答案科目：高中數(shù)學 來源： 題型：
【題目】若圓
關于直線
對稱，則
的最小值為__________．由點
向圓所作兩條切線，切點記為
，當
取最小值時，
外接圓的半徑為__________．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某企業(yè)2018年招聘員工，其中
，
，
，
，
五種崗位的應聘人數(shù)、錄用人數(shù)和錄用比例（精確到1%）如下：
崗位 | 男性 應聘人數(shù) | 男性 錄用人數(shù) | 男性 錄用比例 | 女性 應聘人數(shù) | 女性 錄用人數(shù) | 女性 錄用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
總計 | 533 | 264 |
| 467 | 169 |
|
（1）從表中所有應聘人員中隨機選擇1人，試估計此人被錄用的概率；
（2）從應聘崗位的6人中隨機選擇2人.記
為這2人中被錄用的人數(shù)，求的分布列和數(shù)學期望；
（3）表中，，，，各崗位的男性、女性錄用比例都接近（二者之差的絕對值不大于
），但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發(fā)現(xiàn)，若只考慮其中某四種崗位，則男性、女性的總錄用比例也接近，請寫出這四種崗位.（只需寫出結論）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知集合A＝{x|x2﹣2x﹣3≤0}，B＝{x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}．
（1）若A∪B＝A，求實數(shù)m的取值；
（2）若A∩B＝{x|0≤x≤3}，求實數(shù)m的值；
（3）若A
，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設橢圓
的右焦點為
，離心率為
，過點且與
軸垂直的直線被橢圓截得的線段長為
.
（1）求橢圓
的方程;
（2）若
上存在兩點
，橢圓上存在兩個
點滿足：
三點共線，
三點共線，且
，求四邊形
的面積的最小值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知定義在R上的偶函數(shù)f(x)和奇函數(shù)g(x)滿足
.
(1)求函數(shù)f(x)和g(x)的表達式；
(2)當
時，不等式
恒成立，求實數(shù)a的取值范圍；
(3)若方程
在
上恰有一個實根，求實數(shù)m的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某中學團委組織了“弘揚奧運精神，愛我中華”的知識競賽，從參加考試的學生中抽出60名學生，將其成績(均為整數(shù))分成六段[40,50)，[50,60)，…，[90,100]后畫出如下部分頻率分布直方圖．觀察圖形給出的信息，回答下列問題：
(1)求第四小組的頻率，并補全這個頻率分布直方圖；
(2)估計這次考試的及格率(60分及以上為及格)和平均分；
(3)從成績是[40,50)和[90,100]的學生中選兩人，求他們在同一分數(shù)段的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】共享單車已成為一種時髦的新型環(huán)保交通工具，某共享單車公司為了拓展市場，對
兩個品牌的共享單車在編號分別為
的五個城市的用戶人數(shù)（單位：十萬）進行統(tǒng)計，得到數(shù)據(jù)如下：
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
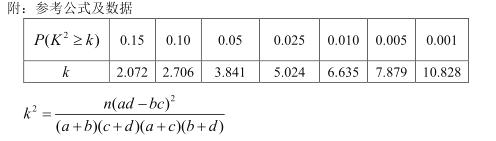
（Ⅰ）若共享單車用戶人數(shù)超過50萬的城市稱為“優(yōu)城”，否則稱為“非優(yōu)城”，據(jù)此判斷能否有85%的把握認為“優(yōu)城”和共享單車品牌有關？
（Ⅱ）若不考慮其它因素，為了拓展市場，對A品牌要從這五個城市選擇三個城市進行宣傳，
（ⅰ）求城市2被選中的概率；
（ⅱ）求在城市2被選中的條件下城市3也被選中的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
.
（1）若函數(shù)
的圖像與
軸無交點，求
的取值范圍；
（2）若方程
在區(qū)間
上存在實根，求的取值范圍；
（3）設函數(shù)
，
，當
時若對任意的
，總存在
，使得
，求
的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
