
【題目】已知函數![]() ,其中
,其中![]() 表示不超過
表示不超過![]() 的最大整數,下列關于
的最大整數,下列關于![]() 說法正確的有:______.
說法正確的有:______.
①![]() 的值域為[-1,1]
的值域為[-1,1]
②![]() 為奇函數
為奇函數
③![]() 為周期函數,且最小正周期T=4
為周期函數,且最小正周期T=4
④![]() 在[0,2)上為單調增函數
在[0,2)上為單調增函數
⑤![]() 與
與![]() 的圖像有且僅有兩個公共點
的圖像有且僅有兩個公共點
科目:高中數學 來源: 題型:
【題目】一個盒子里裝有標號為![]() 的
的![]() 張標簽,隨機的選取兩張標簽.
張標簽,隨機的選取兩張標簽.
(1)若標簽的選取是無放回的,求兩張標簽上的數字為相鄰整數的概率;
(2)若標簽的選取是有放回的,求兩張標簽上的數字至少有一個為5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx![]() .
.
(1)若a=4,求函數f(x)的單調區間;
(2)若函數f(x)在區間(0,1]內單調遞增,求實數a的取值范圍;
(3)若x1、x2∈R+,且x1≤x2,求證:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市100000名職業中學高三學生參加了一項綜合技能測試,從中隨機抽取100名學生的測試成績,制作了以下的測試成績![]() (滿分是184分)的頻率分布直方圖.
(滿分是184分)的頻率分布直方圖.
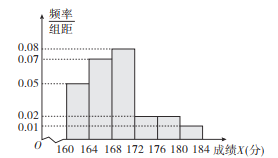
在頻率分布直方圖的分組中,以各組的區間中點值代表該組的各個值,測試成績![]() 落入該區間的頻率作為測試成績取該區間中點值的概率.已知甲、乙兩名學生的測試成績分別為168分和170分.
落入該區間的頻率作為測試成績取該區間中點值的概率.已知甲、乙兩名學生的測試成績分別為168分和170分.
(1)求技能測試成績![]() 的中位數
的中位數![]() ,對甲、乙的成績作出客觀的評價;
,對甲、乙的成績作出客觀的評價;
(2)若市教育局把這次技能測試看作技能大比武,且作出以下獎勵規定:
給測試成績![]() 者頒發獎金
者頒發獎金![]() 元,
元,
給測試成績![]() 者頒發獎金元
者頒發獎金元![]() ,求
,求![]() ;
;
(3)若市教育局把這次技能看作是畢業過關測試,且作出以下規定:
當測試成績![]() 時,統一交測試費和補測費300元;
時,統一交測試費和補測費300元;
當測試成績![]() 時,統一交測試費100元;
時,統一交測試費100元;
當測試成績![]() 時,免交測試費且頒發500元獎金.
時,免交測試費且頒發500元獎金.
若![]() ,據此統計:每個測試者平均最多應該交給教育局多少元?
,據此統計:每個測試者平均最多應該交給教育局多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸標準煤)的幾組對照數據
(噸標準煤)的幾組對照數據
|
|
|
|
|
|
|
|
|
|
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據1求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
(附:![]() ,
,![]() ,
,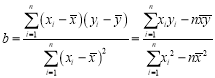 ,
,![]() ,其中
,其中![]() ,
,![]() 為樣本平均值)
為樣本平均值)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業三月中旬生產![]() ,
,![]() ,
,![]() 三種產品共3000件,根據分層隨機抽樣的結果,企業統計員制作了如下的統計表格:
三種產品共3000件,根據分層隨機抽樣的結果,企業統計員制作了如下的統計表格:
產品類別 |
|
|
|
產品數量 | 1300 | ||
樣本中的數量 | 130 |
由于不小心,表格中![]() ,
,![]() 產品的有關數據已被污染得看不清楚,統計員只記得樣本中
產品的有關數據已被污染得看不清楚,統計員只記得樣本中![]() 產品的數量比樣本中
產品的數量比樣本中![]() 產品的數量多10.根據以上信息,求該企業生產
產品的數量多10.根據以上信息,求該企業生產![]() 產品的數量.
產品的數量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() ,
, ![]() .
.
(1)求證:對![]() ,直線
,直線![]() 與圓
與圓![]() 總有兩個不同的交點
總有兩個不同的交點![]() ;
;
(2)求弦![]() 的中點
的中點![]() 的軌跡方程,并說明其軌跡是什么曲線;
的軌跡方程,并說明其軌跡是什么曲線;
(3)是否存在實數![]() ,使得原
,使得原![]() 上有四點到直線
上有四點到直線![]() 的距離為
的距離為![]() ?若存在,求出
?若存在,求出![]() 的范圍;若不存在,說明理由.
的范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只口袋有形狀大小質地都相同的![]() 只小球,這
只小球,這![]() 只小球上分別標記著數字
只小球上分別標記著數字![]() .
.
甲乙丙三名學生約定:
(![]() )每個不放回地隨機摸取一個球;
)每個不放回地隨機摸取一個球;
(![]() )按照甲乙丙的次序一次摸取;
)按照甲乙丙的次序一次摸取;
(![]() )誰摸取的球的數字對打,誰就獲勝.
)誰摸取的球的數字對打,誰就獲勝.
用有序數組![]() 表示這個試驗的基本事件,例如:
表示這個試驗的基本事件,例如:![]() 表示在一次試驗中,甲摸取的是數字
表示在一次試驗中,甲摸取的是數字![]() ,乙摸取的是數字
,乙摸取的是數字![]() ,丙摸取的是數字
,丙摸取的是數字![]() ;
;![]() 表示在一次實驗中,甲摸取的是數
表示在一次實驗中,甲摸取的是數![]() ,乙摸取的是數字
,乙摸取的是數字![]() ,丙摸取的是數字
,丙摸取的是數字![]() .
.
(Ⅰ)列出基本事件,并指出基本事件的總數;
(Ⅱ)求甲獲勝的概率;
(Ⅲ)寫出乙獲勝的概率,并指出甲乙丙三名同學獲勝的概率與其摸取的次序是否有關?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com