
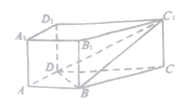
【題目】如圖,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 平面
平面![]() ,若存在,請確定點
,若存在,請確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
【答案】(1)證明見解析;(2)存在點![]() 是
是![]() 的中點,使
的中點,使![]() 平面
平面![]() .
.
【解析】試題分析:(1)先由棱柱的性質(zhì)證明![]() ,再根據(jù)勾股定理可得
,再根據(jù)勾股定理可得![]() ,從而可得
,從而可得![]() 平面
平面![]() ,進而根據(jù)面面垂直的判定定理即可證明平面
,進而根據(jù)面面垂直的判定定理即可證明平面![]() 平面
平面![]() ;(2)存在點
;(2)存在點![]() 是
是![]() 的中點,使
的中點,使![]() 平面
平面![]() ,先根據(jù)中位線定理及平行四邊形的性質(zhì)可得
,先根據(jù)中位線定理及平行四邊形的性質(zhì)可得![]() ,根據(jù)線面平行的判定定理進行證明可得到結(jié)論.
,根據(jù)線面平行的判定定理進行證明可得到結(jié)論.
試題解析:(1)因為![]() 底面
底面![]() , 所以
, 所以![]() 底面
底面![]() ,因為
,因為![]() 底面
底面![]() ,
,
所以![]() 因為底面
因為底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]()
因為![]() ,所以
,所以![]() ,
,![]() 所以
所以![]() ,
,![]()
所以在![]() 中,
中,![]() 所以
所以![]() 所以
所以![]()
又因為![]() 所以
所以![]() 平面
平面![]() 因為
因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
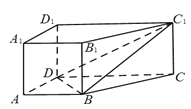
(2)存在點![]() 是
是![]() 的中點,使
的中點,使![]() 平面
平面![]() .
.
證明如下:取線段![]() 的中點為點
的中點為點![]() ,連結(jié)
,連結(jié)![]() ,所以
,所以![]() ,且
,且![]() 因為
因為![]() ,
,![]() 所以
所以![]() ,且
,且![]() 所以四邊形
所以四邊形![]() 是平行四邊形.所以
是平行四邊形.所以![]()
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
【方法點晴】本題主要考查線面平行的判定定理、線面垂直與面面垂直的判定,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關(guān)鍵是設(shè)法在平面內(nèi)找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質(zhì)或者構(gòu)造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質(zhì),即兩平面平行,在其中一平面內(nèi)的直線平行于另一平面.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,直線y=x+2過橢圓C的左焦點F1.
,直線y=x+2過橢圓C的左焦點F1.
(1)求橢圓C的標準方程;
(2)設(shè)過點A(0,﹣1)的直線l與橢圓交于不同兩點M、N,當△MON的面積為![]() 時,求直線l的方程.
時,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義:已知函數(shù)f(x)在[m,n](m<n)上的最小值為t,若t≤m恒成立,則稱函數(shù)f(x)在[m,n](m<n)上具有“DK”性質(zhì).例如函數(shù) ![]() 在[1,9]上就具有“DK”性質(zhì).
在[1,9]上就具有“DK”性質(zhì).
(1)判斷函數(shù)f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性質(zhì)?說明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性質(zhì),求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)討論函數(shù)![]() 極值點的個數(shù),并說明理由;
極值點的個數(shù),并說明理由;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的最大整數(shù)值.
的最大整數(shù)值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)如今網(wǎng)上購物已經(jīng)習以為常,變成人們?nèi)粘I畹囊徊糠郑瑳_擊著人們的傳統(tǒng)消費習慣、思維和生活方式,以其特殊的優(yōu)勢而逐漸深入人心.某市場調(diào)研機構(gòu)對在“雙十一”購物的![]() 名年齡在
名年齡在![]() 歲的消費者進行了年齡段和性別分布的調(diào)查,其部分結(jié)果統(tǒng)計如下表:
歲的消費者進行了年齡段和性別分布的調(diào)查,其部分結(jié)果統(tǒng)計如下表:
年齡(歲) |
|
|
|
|
|
女 | 70 | 50 | 40 | 30 | 20 |
男 | 30 |
| 20 | 15 | 10 |
(1)若按年齡用分層抽樣的方法抽取84個人,其中在![]() 內(nèi)抽取了36人,求
內(nèi)抽取了36人,求![]() 的值.
的值.
(2)在(1)的條件下,用分層抽樣的方法在![]() 歲的消費者中抽取一個容量為8的本,將該樣本看成一個總體,從中任取3人,記
歲的消費者中抽取一個容量為8的本,將該樣本看成一個總體,從中任取3人,記![]() 表示抽得女性消費者的人數(shù),求隨機變量
表示抽得女性消費者的人數(shù),求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(log2x)=x2+2x.
(1)求函數(shù)f(x)的解析式;
(2)若方程f(x)=a2x﹣4在區(qū)間(0,2)內(nèi)有兩個不相等的實根,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分14分)已知遞增等差數(shù)列![]() 中的
中的![]() 是函數(shù)
是函數(shù)![]() 的兩個零點.數(shù)列
的兩個零點.數(shù)列![]() 滿足,點
滿足,點![]() 在直線
在直線![]() 上,其中
上,其中![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項和.
項和.
(1)求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令![]() ,求數(shù)列
,求數(shù)列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com