
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的極值;
的極值;
(2)若![]() ,
, ![]() 是方程
是方程![]() (
(![]() )的兩個不同的實數(shù)根,求證:
)的兩個不同的實數(shù)根,求證: ![]() .
.
【答案】(1)![]() 有極小值
有極小值![]() ,無極大值.(2)見解析
,無極大值.(2)見解析
【解析】試題分析:
(1)求出導(dǎo)函數(shù)![]() ,再求出
,再求出![]() 的零點,確定零點兩側(cè)
的零點,確定零點兩側(cè)![]() 的正負,得極值;
的正負,得極值;
(2)關(guān)鍵是參數(shù)![]() 的轉(zhuǎn)換,由
的轉(zhuǎn)換,由![]() 是某方程的解,代入得
是某方程的解,代入得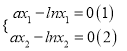 ,兩式相減可解得
,兩式相減可解得 ,這樣要證的不等式即為證
,這樣要證的不等式即為證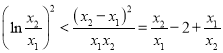 ,這樣可用換元法,設(shè)
,這樣可用換元法,設(shè)![]() ,且不妨役
,且不妨役![]() ,于是有
,于是有![]() ,只要證
,只要證![]() ,此時又可轉(zhuǎn)化為求函數(shù)
,此時又可轉(zhuǎn)化為求函數(shù)![]() 的最大值,求出
的最大值,求出![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() ,
, ![]() ,為確定
,為確定![]() 的正負及零點,可對函數(shù)
的正負及零點,可對函數(shù)![]() 求導(dǎo),利用導(dǎo)數(shù)確定它的單調(diào)性,最終確定
求導(dǎo),利用導(dǎo)數(shù)確定它的單調(diào)性,最終確定![]() 的單調(diào)性,從而得出結(jié)論.
的單調(diào)性,從而得出結(jié)論.
試題解析:
(1)依題意, ![]()
![]()
故當(dāng)![]() 時,
時, ![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]()
故當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有極小值
有極小值![]() ,無極大值.
,無極大值.
(2)因為![]() ,
, ![]() 是方程
是方程![]() 的兩個不同的實數(shù)根.
的兩個不同的實數(shù)根.
∴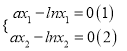 兩式相減得
兩式相減得![]() ,解得
,解得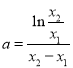
要證: ![]() ,即證:
,即證: ![]() ,即證:
,即證: 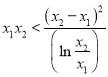 ,
,
即證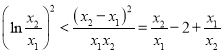 ,
,
不妨設(shè)![]() ,令
,令![]() .只需證
.只需證![]() .
.
設(shè)![]() ,∴
,∴![]() ;
;
令![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴![]()
![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 為減函數(shù),∴
為減函數(shù),∴![]() .
.
即![]() 在
在![]() 恒成立,∴原不等式成立,即
恒成立,∴原不等式成立,即![]() .
.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù),且當(dāng)
上的偶函數(shù),且當(dāng)![]() 時,
時, ![]() .現(xiàn)已畫出函數(shù)
.現(xiàn)已畫出函數(shù)![]() 在
在![]() 軸左側(cè)的圖象,如圖所示,并根據(jù)圖象:
軸左側(cè)的圖象,如圖所示,并根據(jù)圖象:

(1)直接寫出函數(shù)![]() ,
, ![]() 的增區(qū)間;
的增區(qū)間;
(2)寫出函數(shù)![]() ,
, ![]() 的解析式;
的解析式;
(3)若函數(shù)![]() ,
, ![]() ,求函數(shù)
,求函數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正方體ABCD-A1B1C1D1的棱長為2,E為棱CC1的中點,點M在正方形BCC1B1內(nèi)運動,且直線AM//平面A1DE,則動點M 的軌跡長度為( )
A. ![]() B. π C. 2 D.
B. π C. 2 D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
⑴若![]() 的定義域為
的定義域為![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
⑵當(dāng)![]() ,求函數(shù)
,求函數(shù)![]() 的最小值
的最小值![]() ;
;
⑶是否存在實數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,則說明理由.
的值;若不存在,則說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,若橢圓上一點
,若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]()
![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作
作![]() 軸的垂線,交橢圓
軸的垂線,交橢圓![]() 于
于![]() ,求證:
,求證: ![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著資本市場的強勢進入,互聯(lián)網(wǎng)共享單車“忽如一夜春風(fēng)來”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調(diào)查機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)查的網(wǎng)友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
市的使用情況,某調(diào)查機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)查的網(wǎng)友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
經(jīng)常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據(jù)以上數(shù)據(jù),能否在犯錯誤的概率不超過0.15的前提下認為![]() 市使用共享單車情況與年齡有關(guān)?
市使用共享單車情況與年齡有關(guān)?
(2)現(xiàn)從所有抽取的30歲以上的網(wǎng)民中利用分層抽樣抽取5人,
![]() 求這5人中經(jīng)常使用、偶爾或不用共享單車的人數(shù);
求這5人中經(jīng)常使用、偶爾或不用共享單車的人數(shù);
![]() 從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經(jīng)常使用共享單車的概率.
從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經(jīng)常使用共享單車的概率.
參考公式: 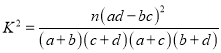 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商店經(jīng)營的某種消費品的進價為每件14元,月銷售量![]() (百件)與每件的銷售價格
(百件)與每件的銷售價格![]() (元)的關(guān)系如圖所示,每月各種開支2 000元.
(元)的關(guān)系如圖所示,每月各種開支2 000元.

(1)寫出月銷售量![]() (百件)關(guān)于每件的銷售價格
(百件)關(guān)于每件的銷售價格![]() (元)的函數(shù)關(guān)系式.
(元)的函數(shù)關(guān)系式.
(2)寫出月利潤![]() (元)與每件的銷售價格
(元)與每件的銷售價格![]() (元)的函數(shù)關(guān)系式.
(元)的函數(shù)關(guān)系式.
(3)當(dāng)該消費品每件的銷售價格為多少元時,月利潤最大?并求出最大月利潤.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com