Question

【題目】已知函數(shù)是偶函數(shù)．

（1）求實數(shù)k的值；

（2）設函數(shù)，若方程只有一個實數(shù)根，求實數(shù)m的取值范圍．

Answer 1

【答案】（1）；（2）或．

【解析】

（1）根據(jù)偶函數(shù)的定義，即可求出；

（2）先將方程化簡可得，，換元，令，得，然后由函數(shù)的定義域確定方程中的范圍，進而得到的范圍，所以在該范圍內(nèi)只有一個解，分類討論，再根據(jù)一元二次方程有解的條件，二次函數(shù)的有關性質(zhì)，零點存在性定理，即可求出．

（1）由是偶函數(shù)．則恒成立，

即．

，

，

．

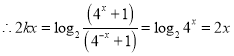（2）方程只有一個根，

則關于x的方程只有一個解，

令，得：

因為中，，則

當時，需要，則；

當時，需要，則，

設，當時，對稱軸方程為

令，若，得，或．

①當時，，拋物線開口向上，此時，，，

所以在上有唯一解，即滿足題意．

②當時，即時，由得，不滿足題意．

③當時，，，且，

所以在上無解，不滿足題意．

④當且時，，則無解，不滿足題意．

⑤當時，且，，，

此時在上有唯一解，即滿足題意．

⑥當時，，且，又，，

所以在上有兩個不等實根，即不滿足題意．

綜上所述，m的取值范圍是或．