
【題目】已知Sn為等差數列{an}的前n項和,且a1=﹣15,S5=﹣55.
(1)求數列{an}的通項公式;
(2)若不等式Sn>t對于任意的n∈N*恒成立,求實數t的取值范圍.
【答案】
(1)解:設等差數列{an}的公差為d,
則由a1=﹣15, ![]() ,
,
得﹣15×5+10d=﹣55,
解得d=2,
∴an=﹣15+(n﹣1)2=2n﹣17,
∴數列{an}的通項公式為an=2n﹣17.
(2)解:由(1)得 ![]() ,
,
∵ ![]() ,
,
∴對于任意的n∈N*,Sn≥﹣64恒成立,
∴若不等式Sn>t對于任意的n∈N*恒成立,則只需t<﹣64,
因此所求實數t的取值范圍為(﹣∞,﹣64)
【解析】(1)利用等差數列的通項公式及其求和公式即可得出.(2)利用等差數列的求和公式、二次函數的單調性即可得出.
【考點精析】根據題目的已知條件,利用數列的前n項和和數列的通項公式的相關知識可以得到問題的答案,需要掌握數列{an}的前n項和sn與通項an的關系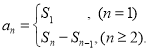 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知動圓C過點(1,0),且于直線x=﹣1相切.
(1)求圓心C的軌跡M的方程;
(2)A,B是M上的動點,O是坐標原點,且![]()
![]()
![]() , 求證:直線AB過定點,并求出該點坐標.
, 求證:直線AB過定點,并求出該點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017寧夏石嘴山市二模】如圖,在以![]() 為頂點的多面體中,
為頂點的多面體中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)請在圖中作出平面![]() ,使得
,使得![]() ,且
,且![]() ,并說明理由;
,并說明理由;
(2)求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某大學一年級女生中,選取身高分別是150cm、155cm、160cm、165cm、170cm的學生各一名,其身高和體重數據如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
體重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y關于x的線性回歸方程;
(2)利用(1)中的回歸方程,計算身高為168cm時,體重的估計值 ![]() 為多少?
為多少?
參考公式:線性回歸方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 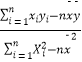 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017福建4月質檢】如圖,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分別為棱
分別為棱![]() 的中點.
的中點.
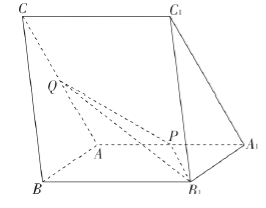
(1)在平面![]() 內過點
內過點![]() 作
作![]() 平面
平面![]() 交
交![]() 于點
于點![]() ,并寫出作圖步驟,但不要求證明.
,并寫出作圖步驟,但不要求證明.
(2)若側面![]() 側面
側面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x2+y2﹣4x﹣2y﹣k=0表示圖形為圓.
(1)若已知曲線關于直線x+y﹣4=0的對稱圓與直線6x+8y﹣59=0相切,求實數k的值;
(2)若k=15,求過該曲線與直線x﹣2y+5=0的交點,且面積最小的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,BC=2,原點O是BC的中點,點A的坐標為 ( ![]() ,0),點D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),點D在平面yOz上,且∠BDC=90°,∠DCB=30°. 
(1)求向量 ![]() 的坐標
的坐標
(2)求向量 ![]() 的夾角的余弦值大小.
的夾角的余弦值大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com