Question

【題目】若正三棱臺 的上、下底面邊長分別為 和 ，高為1，則該正三棱臺的外接球的表面積為 ．

Answer 1

【答案】
【解析】如圖所示， 分別為上下底面的外心，則外接球球心O則在線 上，連接 并延長交 于D1 ， 連接C 并延長交AB于D ，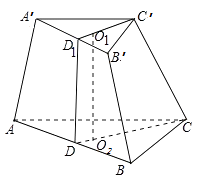

∵等邊三角形 的邊長為 cm,∴ ，
∵等邊三角形ABC的邊長為 cm,∴ C= CD= cm ，
若點 在線段由 上，則 ，
得 ，無解.
若點 在線段由 外，則 ，
得 ，，解得 .
則該正三棱臺的外接球的表面積為 .
故答案為： .
考查正三棱臺的外接球的表面積的求法，考查正三棱臺及其外接球等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、函數與方程思想．研究球與多面體的接、切問題主要考慮以下幾個方面的問題：
（1）球心與多面體中心的位置關系；
（2）球的半徑與多面體的棱長的關系；
（3）球自身的對稱性與多面體的對稱性；
（4）能否做出軸截面．