
【題目】已知函數(shù)![]() .(
.( ![]() )
)
(I)試確定函數(shù)![]() 的零點(diǎn)個(gè)數(shù);
的零點(diǎn)個(gè)數(shù);
(II)設(shè)![]() 是函數(shù)
是函數(shù)![]() 的兩個(gè)零點(diǎn),當(dāng)
的兩個(gè)零點(diǎn),當(dāng)![]() 時(shí),求
時(shí),求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見(jiàn)解析;(Ⅱ) ![]() .
.
【解析】試題分析:(I)函數(shù)![]() 的零點(diǎn)即方程
的零點(diǎn)即方程![]() 的根,變形為
的根,變形為![]() ,令
,令![]() ,根據(jù)圖像特征討論即可;
,根據(jù)圖像特征討論即可;
(II)根據(jù)![]() 是函數(shù)
是函數(shù)![]() 的兩個(gè)零點(diǎn),得
的兩個(gè)零點(diǎn),得![]() (
(![]() ),
),![]() (
(![]() ),得
),得![]()
![]()
![]()
 ,進(jìn)而利用
,進(jìn)而利用![]() 求范圍即可.
求范圍即可.
試題解析:

解法1:(I)函數(shù)![]() 的零點(diǎn)即方程
的零點(diǎn)即方程![]() 的根,
的根,
由![]() 得
得![]() ,令
,令![]() ,
,
則![]() ,--------------------2分
,--------------------2分
由![]() 得
得![]() ,∴函數(shù)
,∴函數(shù)![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
由![]() 得
得![]() ,∴函數(shù)
,∴函數(shù)![]() 在
在![]() 上單調(diào)遞減,----3分
上單調(diào)遞減,----3分
∴當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有最大值,
有最大值, ![]() ,
,
又當(dāng)![]() 時(shí),
時(shí), ![]() >0,當(dāng)
>0,當(dāng)![]() 時(shí)
時(shí)![]() ;
;
當(dāng)![]() 時(shí)
時(shí)![]() >0,
>0, ![]() ,當(dāng)
,當(dāng)![]() 時(shí)
時(shí)![]() ,
,
∴當(dāng)![]() 時(shí),
時(shí), ![]() 與
與![]() 只有一個(gè)公共點(diǎn),從而函數(shù)
只有一個(gè)公共點(diǎn),從而函數(shù)![]() 有一個(gè)零點(diǎn);
有一個(gè)零點(diǎn);
當(dāng)![]() 時(shí),
時(shí), ![]() 與
與![]() 有兩個(gè)公共點(diǎn),從而函數(shù)
有兩個(gè)公共點(diǎn),從而函數(shù)![]() 有兩個(gè)零點(diǎn).
有兩個(gè)零點(diǎn).
(II)設(shè)![]() 由(I)知
由(I)知![]() 且
且![]() ,
,
由![]() ,得
,得![]() (
(![]() )
)
由![]() ,得
,得![]() (
(![]() )
)
∴![]()
![]()
![]()
 ,
,
∵![]() ∴
∴![]() ,
, ![]() ,(兩者僅當(dāng)
,(兩者僅當(dāng)![]() 時(shí)取等號(hào))
時(shí)取等號(hào))
∴![]() ,又
,又![]() ,
,
∴ ,
,
∴![]() ,
,
由![]() 得
得![]() .
.
解法2:(I)∵![]() ,
, ![]() 不是函數(shù)的零點(diǎn);
不是函數(shù)的零點(diǎn);
當(dāng)![]() 時(shí),由
時(shí),由![]() 得
得![]()
設(shè)![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上單調(diào)遞減,
上單調(diào)遞減,
當(dāng)![]() 且
且![]() 時(shí),
時(shí), ![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí), ![]() ;
;
當(dāng)![]() 且
且![]() 時(shí),
時(shí), ![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí), ![]() ;
;
當(dāng)![]() 時(shí),由
時(shí),由![]() ,有
,有![]() ,
,
當(dāng)![]() 時(shí),有
時(shí),有![]() ,
, ![]() ,
,
所以當(dāng)![]() 時(shí),曲線
時(shí),曲線![]() 與
與![]() 只一個(gè)公共點(diǎn),函數(shù)
只一個(gè)公共點(diǎn),函數(shù)![]() 有一個(gè)零點(diǎn);
有一個(gè)零點(diǎn);
當(dāng)![]() 時(shí),曲線
時(shí),曲線![]() 與
與![]() 有兩個(gè)公共點(diǎn),函數(shù)
有兩個(gè)公共點(diǎn),函數(shù)![]() 有兩個(gè)零點(diǎn);
有兩個(gè)零點(diǎn);
(II)不妨設(shè)![]() ,由(I)得
,由(I)得![]() ,且
,且![]() ,
, ![]() ,
,
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,
,
∴![]()
![]()
![]()
 ,
,
∵![]() ∴
∴![]() ,
, ![]() ,(兩者僅當(dāng)
,(兩者僅當(dāng)![]() 時(shí)取等號(hào))
時(shí)取等號(hào))
∴![]() ,又
,又![]() ,
,
∴ ,
,
∴![]() ,由
,由![]() 得
得![]() .
.


 寒假樂(lè)園北京教育出版社系列答案
寒假樂(lè)園北京教育出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某手機(jī)生產(chǎn)企業(yè)為了解消費(fèi)者對(duì)某款手機(jī)功能的認(rèn)同情況,通過(guò)銷售部隨機(jī)抽取50名購(gòu)買該款手機(jī)的消費(fèi)者,并發(fā)出問(wèn)卷調(diào)查(滿分50分),該問(wèn)卷只有30份給予回復(fù),這30份的評(píng)分如下:

(Ⅰ)完成下面的莖葉圖,并求16名男消費(fèi)者評(píng)分的中位數(shù)與14名女消費(fèi)者評(píng)分的平均值;

(Ⅱ)若大于40分為“滿意”,否則為“不滿意”,完成上面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為消費(fèi)者對(duì)該款手機(jī)的“滿意度”與性別有關(guān).
的把握認(rèn)為消費(fèi)者對(duì)該款手機(jī)的“滿意度”與性別有關(guān).
參考公式:  ,其中
,其中![]()
參考數(shù)據(jù):

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】關(guān)于二項(xiàng)式(x-1)2005有下列命題:
①該二項(xiàng)展開(kāi)式中非常數(shù)項(xiàng)的系數(shù)和是1;
②該二項(xiàng)展開(kāi)式中第六項(xiàng)為![]() x1999;
x1999;
③該二項(xiàng)展開(kāi)式中系數(shù)最大的項(xiàng)是第1002項(xiàng);
④當(dāng)x=2006時(shí),(x-1)2005除以2006的余數(shù)是2005。
其中正確命題的序號(hào)是__________。(注:把你認(rèn)為正確的命題序號(hào)都填上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
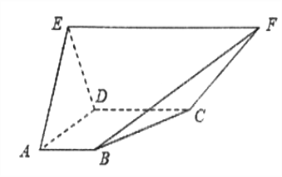
【題目】(本小題滿分12分)在如圖所示的五面體中,面![]() 為直角梯形,
為直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是邊長(zhǎng)為2的正三角形.
是邊長(zhǎng)為2的正三角形.
(1)證明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)討論![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)設(shè)![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(Ⅲ)設(shè)![]() 是
是![]() 的兩個(gè)零點(diǎn),證明
的兩個(gè)零點(diǎn),證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】小張同學(xué)計(jì)劃在期末考試結(jié)束后,和其他小伙伴一塊兒外出旅游,增長(zhǎng)見(jiàn)識(shí).旅行社為他們提供了省內(nèi)的都江堰、峨眉山、九寨溝和省外的麗江古城,黃果樹(shù)瀑布和鳳凰古城這六個(gè)景點(diǎn),由于時(shí)間和距離等原因,只能從中任取4個(gè)景點(diǎn)進(jìn)行參觀,其中黃果樹(shù)瀑布不能第一個(gè)參觀,且最后參觀的是省內(nèi)景點(diǎn),則不同的旅游順序有( )
A. 54種 B. 72種 C. 120種 D. 144種
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在 ![]() 上的函數(shù)
上的函數(shù) ![]() 若同時(shí)滿足:①存在
若同時(shí)滿足:①存在 ![]() ,使得對(duì)任意的
,使得對(duì)任意的 ![]() ,都有
,都有 ![]() ;②
;② ![]() 的圖象存在對(duì)稱中心.則稱
的圖象存在對(duì)稱中心.則稱 ![]() 為“
為“![]() 函數(shù)”.已知函數(shù)
函數(shù)”.已知函數(shù) ![]() 和
和 ![]() ,則以下結(jié)論一定正確的是
,則以下結(jié)論一定正確的是 ![]()
A. ![]() 和
和 ![]() 都是
都是 ![]() 函數(shù) B.
函數(shù) B. ![]() 是
是 ![]() 函數(shù),
函數(shù), ![]() 不是
不是 ![]() 函數(shù)
函數(shù)
C. ![]() 不是
不是 ![]() 函數(shù),
函數(shù), ![]() 是
是 ![]() 函數(shù) D.
函數(shù) D. ![]() 和
和 ![]() 都不是
都不是 ![]() 函數(shù)
函數(shù)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com