Question

【題目】已知函數，；.

（1）求的最大值；

（2）若對，總存在使得成立，求的取值范圍；

（3）證明不等式.

Answer 1

【答案】

【解析】

試題分析：

（1）對函數求導，，時，，當時，，函數單調遞增，當時，，函數單調遞減，所以當時，函數取得極大值，也是最大值，所以的最大值為；

（2）若對，總存在使得成立，則轉化為，由（1）知，問題轉化為求函數在區間上的最大值，對求導，，分類討論，當時，函數在上恒成立，在上單調遞增，只需滿足，，解得，所以；當時，時，（舍），當時，在上恒成立，只需滿足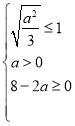，，解得，當，即時，在遞減，遞增，而，在為正，在為負，∴，當，而時，，不合題意，可以求出的取值范圍。

（3）由（1）知：即， 取，∴，

∴，即∴，等號右端為等比數列求和。

試題解析：（1）∵，

∴，

∴當時，，時，，

∴，∴的最大值為.

（2），使得成立，等價于

由（1）知，，當時，在時恒為正，滿足題意.

當時，，令，解得，

∴在上單調遞減，在上單調遞增，

若，即時，，∴，∴.

若，即時，在遞減，遞增，而，在為正，在為負，∴，

當，而時，，不合題意，

綜上的取值范圍為.

（3）由（1）知：即，

取，∴，∴，即

∴

.