
【題目】![]() 的內(nèi)角
的內(nèi)角![]() 、
、![]() 、
、![]() 的對(duì)邊分別為
的對(duì)邊分別為![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),已知
的中點(diǎn),已知![]() ,
,![]() ,
,![]() .
.
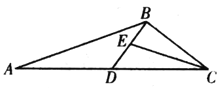
(1)求角![]() 的大小和
的大小和![]() 的長(zhǎng);
的長(zhǎng);
(2)設(shè)![]() 的角平分線交
的角平分線交![]() 于
于![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由三角函數(shù)恒等變換的應(yīng)用化簡(jiǎn)已知等式可得tanC![]() ,結(jié)合范圍C∈(0,π),可求C的值,由余弦定理可得BD的值.
,結(jié)合范圍C∈(0,π),可求C的值,由余弦定理可得BD的值.
(2)由(1)可知BD2+BC2=4=CD2,可求∠DBC![]() ,可得S△DBC
,可得S△DBC![]() ,利用三角形的面積公式可求S△BCE
,利用三角形的面積公式可求S△BCE![]() S△CED,代入S△BCE+S△CED=S△BCD
S△CED,代入S△BCE+S△CED=S△BCD![]() ,即可解得S△CED的值.
,即可解得S△CED的值.
(1)∵由題意可得:![]() sinC+1﹣2sin2
sinC+1﹣2sin2![]() 0,
0,
∴![]() sinC+cos(A+B)=0,
sinC+cos(A+B)=0,
又A+B=π﹣C,
∴![]() sinC﹣cosC=0,可得tanC
sinC﹣cosC=0,可得tanC![]() ,
,
∵C∈(0,π),
∴C![]() ,
,
∴在△BCD中,由余弦定理可得:BD2=3+4﹣2![]() 1,
1,
解得:BD=1,
(2)由(1)可知BD2+BC2=4=CD2,
∴∠DBC![]() ,
,
∴S△DBC![]() BDBC
BDBC![]() ,
,
∵CE是∠BCD的角平分線,
∴∠BCE=∠DCE,
在△CEB和△CED中,S△BCE![]() ,
,
S△CED![]() ,
,
可得:![]() ,
,
∴S△BCE![]() S△CED,
S△CED,
∴代入S△BCE+S△CED=S△BCD![]() ,(1
,(1![]() )S△CED
)S△CED![]() ,
,
∴S△CED![]() (2
(2![]() )=2
)=2![]() 3.
3.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
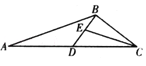
【題目】如圖,在凸四邊形ABCD中,M為邊AB的中點(diǎn),且MC=MD.分別過點(diǎn)C、D作邊BC、AD的垂線,設(shè)兩條垂線的交點(diǎn)為P.過點(diǎn)P作![]() 與Q.求證:
與Q.求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】大學(xué)先修課程,是在高中開設(shè)的具有大學(xué)水平的課程,旨在讓學(xué)有余力的高中生早接受大學(xué)思維方式、學(xué)習(xí)方法的訓(xùn)練,為大學(xué)學(xué)習(xí)乃至未來的職業(yè)生涯做好準(zhǔn)備.某高中成功開設(shè)大學(xué)先修課程已有兩年,共有250人參與學(xué)習(xí)先修課程,這兩年學(xué)習(xí)先修課程的學(xué)生都參加了高校的自主招生考試(滿分100分),結(jié)果如下表所示:
分?jǐn)?shù) |
|
|
|
|
|
人數(shù) | 25 | 50 | 100 | 50 | 25 |
參加自主招生獲得通過的概率 | 0.9 | 0.8 | 0.6 | 0.4 | 0.3 |
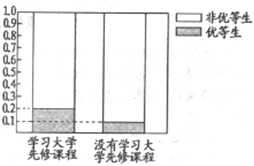
(Ⅰ)這兩年學(xué)校共培養(yǎng)出優(yōu)等生150人,根據(jù)下圖等高條形圖,填寫相應(yīng)列聯(lián)表,并根據(jù)列聯(lián)表檢驗(yàn)?zāi)芊裨诜稿e(cuò)的概率不超過0.01的前提下認(rèn)為學(xué)習(xí)先修課程與優(yōu)等生有關(guān)系?
優(yōu)等生 | 非優(yōu)等生 | 總計(jì) | |
學(xué)習(xí)大學(xué)先修課程 | 250 | ||
沒有學(xué)習(xí)大學(xué)先修課程 | |||
總計(jì) | 150 |
(Ⅱ)已知今年全校有150名學(xué)生報(bào)名學(xué)習(xí)大學(xué)選項(xiàng)課程,并都參加了高校的自主招生考試,以前兩年參加大學(xué)先修課程學(xué)習(xí)成績(jī)的頻率作為今年參加大學(xué)先修課程學(xué)習(xí)成績(jī)的概率.
(ⅰ)在今年參與大學(xué)先修課程學(xué)習(xí)的學(xué)生中任取一人,求他獲得高校自主招生通過的概率;
(ⅱ)某班有4名學(xué)生參加了大學(xué)先修課程的學(xué)習(xí),設(shè)獲得高校自主招生通過的人數(shù)為![]() ,求
,求![]() 的分布列,試估計(jì)今年全校參加大學(xué)先修課程學(xué)習(xí)的學(xué)生獲得高校自主招生通過的人數(shù).
的分布列,試估計(jì)今年全校參加大學(xué)先修課程學(xué)習(xí)的學(xué)生獲得高校自主招生通過的人數(shù).
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(題文)已知![]() 是直線
是直線![]() 上的動(dòng)點(diǎn),點(diǎn)
上的動(dòng)點(diǎn),點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 垂直,并且
垂直,并且![]() 與線段
與線段![]() 的垂直平分線相交于點(diǎn)
的垂直平分線相交于點(diǎn)![]() .
.
(1)求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)曲線![]() 上的動(dòng)點(diǎn)
上的動(dòng)點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的另一個(gè)交點(diǎn)為
的另一個(gè)交點(diǎn)為![]() (
(![]() 與
與![]() 不重合),是否存在一個(gè)定點(diǎn)
不重合),是否存在一個(gè)定點(diǎn)![]() ,使得
,使得![]() 三點(diǎn)共線?若存在,求出點(diǎn)
三點(diǎn)共線?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義:區(qū)間![]() ,
,![]() ,
,![]() ,
,![]() 的長(zhǎng)度均為
的長(zhǎng)度均為![]() ,若不等式
,若不等式![]() 的解集是互不相交區(qū)間的并集,設(shè)該不等式的解集中所有區(qū)間的長(zhǎng)度之和為
的解集是互不相交區(qū)間的并集,設(shè)該不等式的解集中所有區(qū)間的長(zhǎng)度之和為![]() ,則( )
,則( )
A. 當(dāng)![]() 時(shí),
時(shí),![]() B. 當(dāng)
B. 當(dāng)![]() 時(shí),
時(shí),![]()
C. 當(dāng)![]() 時(shí),
時(shí),![]() D. 當(dāng)
D. 當(dāng)![]() 時(shí),
時(shí),![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè)![]() ,若
,若![]() ,
,![]() 為函數(shù)
為函數(shù)![]() 的兩個(gè)不同極值點(diǎn),證明:
的兩個(gè)不同極值點(diǎn),證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】求最小的正整數(shù)![]() ,使得當(dāng)正整數(shù)點(diǎn)
,使得當(dāng)正整數(shù)點(diǎn)![]() 時(shí),在前
時(shí),在前![]() 個(gè)正整數(shù)構(gòu)成的集合
個(gè)正整數(shù)構(gòu)成的集合![]() 中,對(duì)任意
中,對(duì)任意![]() 總存在另一個(gè)數(shù)
總存在另一個(gè)數(shù)![]() 且
且![]() ,滿足
,滿足![]() 為平方數(shù).
為平方數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在邊長(zhǎng)為2的菱形![]() 中,
中,![]() ,將菱形
,將菱形![]() 沿對(duì)角線
沿對(duì)角線![]() 對(duì)折,使二面角
對(duì)折,使二面角![]() 的余弦值為
的余弦值為![]() ,則所得三棱錐
,則所得三棱錐![]() 的內(nèi)切球的表面積為( )
的內(nèi)切球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com