
【題目】某高校在2014年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組,得到的頻率分布表如下表所示.
組號 | 分組 | 頻數 | 頻率 |
第1組 | [160,165) | 5 | 0.050 |
第2組 | [165,170) | n | 0.350 |
第3組 | [170,175) | 30 | p |
第4組 | [175,180) | 20 | 0.200 |
第5組 | [180,185] | 10 | 0.100 |
合計 | 100 | 1.000 |
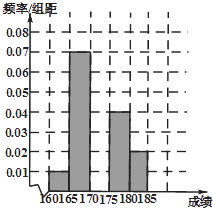
(1)求頻率分布表中n,p的值,并補充完整相應的頻率分布直方圖;
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試,則第3、4、5組每組各抽取多少名學生進入第二輪面試?
(3)在(2)的前提下,學校決定從6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有1名學生被甲考官面試的概率.
【答案】
(1)解:由題意可知,第2組的頻數n=0.35×100=35人,
第3組的頻率p= ![]() ,
,
(2)解:∵第3、4、5組共有60名學生,
∴利用分層抽樣在60名學生中抽取6名學生,
每組分別為:第3組: ![]() ×6=3人,第4組:
×6=3人,第4組: ![]() ×6=2人,第5組:
×6=2人,第5組: ![]() =1人,
=1人,
∴第3、4、5組分別抽取3人、2人、1人
(3)解:試驗發生包含的事件是從六位同學中抽兩位同學有C62=15種
滿足條件的事件是第4組至少有一名學生被考官A面試有C21C41+1=9種結果,
∴至少有一位同學入選的概率為 ![]() =
= ![]()
【解析】(1)根據所給的第二組的頻率,利用頻率乘以樣本容量,得到要求的頻數,再根據所給的頻數,利用頻除以樣本容量,得到要求的頻率.(2)因為在筆試成績高的第3、4、5組中用分層抽樣抽取6名學生,而這三個小組共有60人,利用每一個小組在60人中所占的比例,乘以要抽取的人數,得到結果.(3)試驗發生包含的事件是從六位同學中抽兩位同學有C62種滿足條件的事件是第4組至少有一名學生被考官A面試有C21C41+1種結果,根據古典概型概率公式得到結果.
【考點精析】解答此題的關鍵在于理解頻率分布直方圖的相關知識,掌握頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若對一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個無窮數列![]() 和
和![]() 的前
的前![]() 項和分別為
項和分別為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,對任意的
,對任意的![]() ,都有
,都有![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() 為等差數列,對任意的
為等差數列,對任意的![]() ,都有
,都有![]() .證明:
.證明: ![]() ;
;
(3)若![]() 為等比數列,
為等比數列, ![]() ,
, ![]() ,求滿足
,求滿足![]()
![]() 的
的![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() :
: ![]() (
(![]() 為參數,
為參數, ![]() ),在以坐標原點為極點,
),在以坐標原點為極點, ![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() :
: ![]() .
.
(1)試將曲線![]() 與
與![]() 化為直角坐標系
化為直角坐標系![]() 中的普通方程,并指出兩曲線有公共點時
中的普通方程,并指出兩曲線有公共點時![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,兩曲線相交于
時,兩曲線相交于![]() ,
, ![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐A﹣BCD的各個棱長都相等,E,F分別是棱AB,CD的中點,則EF與BC所成的角是( ) 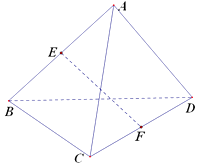
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此做了四次試驗,得到的數據如表:
零件的個數x(個) | 2 | 3 | 4 | 5 |
加工的時間y(小時) | 2.5 | 3 | 4 | 4.5 |
(1)求出y關于x的線性回歸方程 ![]() ;
;
(2)試預測加工10個零件需要多少小時?
(參考公式: ![]() =
= 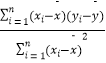 =
= 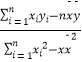 ;
; ![]() ;)
;)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,PD⊥底面ABCD,且底面ABCD是邊長為2的正方形,M、N分別為PB、PC的中點. 
(1)證明:MN∥平面PAD;
(2)若PB與平面ABCD所成的角為45°,求三棱錐C﹣BDN的體積V.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高三年級有學生500人,其中男生300人,女生200人。為了研究學生的數學成績是否與性別有關,采用分層抽樣的方法,從中抽取了100名學生,統計了他們期中考試的數學分數,然后按照性別分為男、女兩組,再將兩組的分數分成5組: ![]() 分別加以統計,得到如圖所示的頻率分布直方圖。
分別加以統計,得到如圖所示的頻率分布直方圖。

(I)從樣本分數小于110分的學生中隨機抽取2人,求兩人恰為一男一女的概率;
(II)若規定分數不小于130分的學生為“數學尖子生”,請你根據已知條件完成2×2列聯表,并判斷是否有90%的把握認為“數學尖子生與性別有關”?
 附表:
附表:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com