
【題目】在![]() ,點M是
,點M是![]() 外一點,BM=2CM=2,則AM的最大值與最小值的差為____________.
外一點,BM=2CM=2,則AM的最大值與最小值的差為____________.
【答案】![]()
【解析】
取邊BC的中點為O,把(![]() )
)![]() 0轉化為
0轉化為![]()
![]() 0,得出
0,得出![]() ⊥
⊥![]() ,△ABC為等邊三角形,以O為坐標原點,以BC邊所在的直線為x軸,建立平面直角坐標系,利用坐標表示得出AM的解析式,求出它的最大值與最小值即可.
,△ABC為等邊三角形,以O為坐標原點,以BC邊所在的直線為x軸,建立平面直角坐標系,利用坐標表示得出AM的解析式,求出它的最大值與最小值即可.
取邊BC的中點為O,則![]() (
(![]() ),
),
又(![]() )
)![]() 0,∴
0,∴![]()
![]() 0,
0,
∴![]() ⊥
⊥![]() ,∴△ABC為等腰三角形,
,∴△ABC為等腰三角形,
又∠A![]() ,∴△ABC為等邊三角形,
,∴△ABC為等邊三角形,
以O為坐標原點,以BC邊所在的直線為x軸,
建立平面直角坐標系如圖所示;
并設BC=2a(![]() a
a![]() ),點M(x,y);
),點M(x,y);
則A(0,![]() a),B(﹣a,0),C(a,0),
a),B(﹣a,0),C(a,0),
又BM=2CM=2,
所以(x+a)2+y2=4
(x﹣a)2+y2=1,
所以解方程組![]() ,
,
解得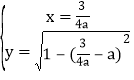 或
或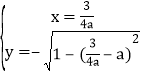 ,
,
所以當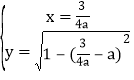 時,
時,

![]()
![]()
![]() ,
,
令a2![]() cosθ,
cosθ,
則AM![]() ,
,
所以當θ![]() 時(AM)min=1,
時(AM)min=1,
同理當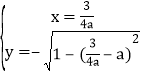 時,
時,
AM![]() ,
,
所以當θ![]() 時(AM)max=3;
時(AM)max=3;
綜上可知:AM的取值范圍是[1,3],
AM的最大值與最小值的差是2.
故答案為:2.


科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
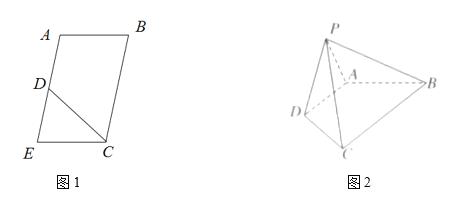
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市10000名職業中學高三學生參加了一項綜合技能測試,從中隨機抽取100名學生的測試成績,制作了以下的測試成績![]() (滿分是184分)的頻率分布直方圖.
(滿分是184分)的頻率分布直方圖.
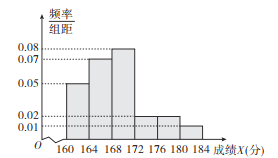
市教育局規定每個學生需要繳考試費100元.某企業根據這100000名職業中學高三學生綜合技能測試成績來招聘員工,劃定的招聘錄取分數線為172分,且補助已經被錄取的學生每個人![]() 元的交通和餐補費.
元的交通和餐補費.
(1)已知甲、乙兩名學生的測試成績分別為168分和170分,求技能測試成績![]() 的中位數,并對甲、乙的成績作出客觀的評價;
的中位數,并對甲、乙的成績作出客觀的評價;
(2)令![]() 表示每個學生的交費或獲得交通和餐補費的代數和,把
表示每個學生的交費或獲得交通和餐補費的代數和,把![]() 用
用![]() 的函數來表示,并根據頻率分布直方圖估計
的函數來表示,并根據頻率分布直方圖估計![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,圓
,圓![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,圓
,圓![]() 在點
在點![]() 處的切線被橢圓
處的切線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設圓![]() 上任意一點
上任意一點![]() 處的切線交橢圓
處的切線交橢圓![]() 于點
于點![]() ,試判斷
,試判斷![]() 是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區觀眾對大型綜藝活動《中國好聲音》的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名.下面是根據調查結果繪制的觀眾收看該節目的場數與所對應的人數表:

將收看該節目場次不低于13場的觀眾稱為“歌迷”,已知“歌迷”中有10名女性.
(1)根據已知條件完成下面的![]() 列聯表,并據此資料我們能否有
列聯表,并據此資料我們能否有![]() 的把握認為“歌迷”與性別有關?
的把握認為“歌迷”與性別有關?

(2)將收看該節目所有場次(14場)的觀眾稱為“超級歌迷”,已知“超級歌迷”中有2名女性,若從“超級歌迷”中任意選取2人,求至少有1名女性觀眾的概率.

附: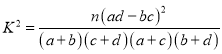 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.自變量取值一定時,因變量的取值有一定隨機性的兩個變量之間的關系叫做相關關系
B.在線性回歸分析中,相關系數![]() 越大,變量間的相關性越強
越大,變量間的相關性越強
C.在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
D.在回歸分析中,![]() 為
為![]() 的模型比
的模型比![]() 為
為![]() 的模型擬合的效果好
的模型擬合的效果好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,直線![]() 的參數方程為
的參數方程為 (其中
(其中![]() 為參數).現以坐標原點為極點,
為參數).現以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 普通方程和曲線
普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() ,且與直線
,且與直線![]() 平行的直線
平行的直線![]() 交
交![]() 于
于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線![]() 的參數方程為
的參數方程為![]() ,
,![]() 為參數
為參數![]() ,在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,曲線
,在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
![]() 求曲線
求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
![]() 若射線l:
若射線l:![]() 與曲線
與曲線![]() ,
,![]() 的交點分別為A,
的交點分別為A,![]() B異于原點
B異于原點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在以原點O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() ,平面直角坐標系xOy中,曲線C的參數方程為
,平面直角坐標系xOy中,曲線C的參數方程為![]() (
(![]() 為參數).
為參數).
(1)設直線l與曲線C交于M,N兩點,求|MN|;
(2)若點P(x,y)為曲線C上任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com