
【題目】已知函數f(x)=![]() ,g(x)=
,g(x)=![]() ,若函數y=f(g(x))+a有三個不同的零點x1,x2,x3(其中x1<x2<x3),則2g(x1)+g(x2)+g(x3)的取值范圍為______.
,若函數y=f(g(x))+a有三個不同的零點x1,x2,x3(其中x1<x2<x3),則2g(x1)+g(x2)+g(x3)的取值范圍為______.
【答案】![]()
【解析】
首先研究函數![]() 和函數
和函數![]() 的性質,然后結合韋達定理和函數的性質求解2g(x1)+g(x2)+g(x3)的取值范圍即可.
的性質,然后結合韋達定理和函數的性質求解2g(x1)+g(x2)+g(x3)的取值范圍即可.
由題意可知:![]() ,
,
將對勾函數![]() 的圖象向右平移一個單位,再向上平移一個單位即可得到函數
的圖象向右平移一個單位,再向上平移一個單位即可得到函數![]() 的圖象,其圖象如圖所示:
的圖象,其圖象如圖所示:

由![]() 可得
可得![]() ,
,
據此可知![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減,
上單調遞減,
繪制函數圖象如圖所示:

則![]() 的最大值為
的最大值為![]() ,
,![]() ,
,
函數y=f(g(x))+a有三個不同的零點,則![]() ,
,
令![]() ,則
,則![]() ,
,
整理可得:![]() ,由韋達定理有:
,由韋達定理有:![]() .
.
滿足題意時,應有:![]() ,
,![]() ,
,
故![]() .
.
【點睛】
本題主要考查導數研究函數的性質,等價轉化的數學思想,復合函數的性質及其應用等知識,意在考查學生的轉化能力和計算求解能力.
【題型】填空題
【結束】
17
【題目】已知等比數列{![]() }的前n項和為
}的前n項和為![]() ,且滿足2
,且滿足2![]() =
=![]() +m(m∈R).
+m(m∈R).
(Ⅰ)求數列{![]() }的通項公式;
}的通項公式;
(Ⅱ)若數列{![]() }滿足
}滿足![]() ,求數列{
,求數列{![]() }的前n項和
}的前n項和![]() .
.
 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫院隨機對入院的50人進行問卷調查,得到了如下的列聯表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合計 | 30 | 20 | 50 |
(Ⅰ)用分層抽樣的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中選2人,求恰好有1名女性的概率;
(Ⅲ)為了研究心肺疾病是否與性別有關,請計算出統計量![]() ,你有多大把握認為心肺疾病與性別有關?(結果保留三個有效數字)
,你有多大把握認為心肺疾病與性別有關?(結果保留三個有效數字)
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024/p> | 6.635 | 7.879 | 10.828 |
參考公式: ![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要得到函數f(x)=2sinxcosx,x∈R的圖象,只需將函數g(x)=2cos2x﹣1,x∈R的圖象( )
A.向左平移 ![]() 個單位
個單位
B.向右平移 ![]() 個單位
個單位
C.向左平移 ![]() 個單位
個單位
D.向右平移 ![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】南宋數學家秦九韶早在《數書九章》中就獨立創造了已知三角形三邊求其面積的公式:“以小斜冪并大斜冪,減中斜冪,余半之,自乘于上,以小斜冪乘大斜冪減之,以四約之,為實,一為從隅,開方得積.”(即:S=![]() ,a>b>c),并舉例“問沙田一段,有三斜(邊),其小斜一十三里,中斜一十四里,大斜一十五里,欲知為田幾何?”則該三角形田面積為
,a>b>c),并舉例“問沙田一段,有三斜(邊),其小斜一十三里,中斜一十四里,大斜一十五里,欲知為田幾何?”則該三角形田面積為
A. 82平方里 B. 84平方里
C. 85平方里 D. 83平方里
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(Ⅰ)請分別求出甲、乙兩種薪酬方案中日薪y(單位:元)與送貨單數n的函數關系式;
(Ⅱ)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數滿足以下條件:在這100天中的派送量指標滿足如圖所示的直方圖,其中當某天的派送量指標在(![]() ,
,![]() ](n=1,2,3,4,5)時,日平均派送量為50+2n單.若將頻率視為概率,回答下列問題:
](n=1,2,3,4,5)時,日平均派送量為50+2n單.若將頻率視為概率,回答下列問題:

①根據以上數據,設每名派送員的日薪為X(單位:元),試分別求出甲、乙兩種方案的日薪X的分布列,數學期望及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由。
(參考數據:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
【答案】(Ⅰ)甲方案的函數關系式為: ![]() ,乙方案的函數關系式為:
,乙方案的函數關系式為:![]() ;(Ⅱ)①見解析,②見解析.
;(Ⅱ)①見解析,②見解析.
【解析】
(Ⅰ)由題意可得甲方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為: ![]() , 乙方案中派送員日薪
, 乙方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為:![]() .
.
(Ⅱ)①由題意求得X的分布列,據此計算可得![]() ,
,![]() ,
,![]() .
.
②答案一:由以上的計算可知,![]() 遠小于
遠小于![]() ,即甲方案日工資收入波動相對較小,所以小明應選擇甲方案.
,即甲方案日工資收入波動相對較小,所以小明應選擇甲方案.
答案二:由以上的計算結果可以看出,![]() ,所以小明應選擇乙方案.
,所以小明應選擇乙方案.
(Ⅰ)甲方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為: ![]() ,
,
乙方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為:![]()
(Ⅱ)①由已知,在這100天中,該公司派送員日平均派送單數滿足如下表格:
單數 | 52 | 54 | 56 | 58 | 60 |
頻率 | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]() 的分布列為:
的分布列為:
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]()
所以![]() 的分布列為:
的分布列為:
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
所以![]()
![]()
②答案一:由以上的計算可知,雖然![]() ,但兩者相差不大,且
,但兩者相差不大,且![]() 遠小于
遠小于![]() ,即甲方案日工資收入波動相對較小,所以小明應選擇甲方案.
,即甲方案日工資收入波動相對較小,所以小明應選擇甲方案.
答案二:由以上的計算結果可以看出,![]() ,即甲方案日工資期望小于乙方案日工資期望,所以小明應選擇乙方案.
,即甲方案日工資期望小于乙方案日工資期望,所以小明應選擇乙方案.
【點睛】
本題主要考查頻率分布直方圖,數學期望與方差的含義與實際應用等知識,意在考查學生的轉化能力和計算求解能力.
【題型】解答題
【結束】
20
【題目】已知橢圓C:![]() (a>b>0)的左、右焦點分別為F1,F2,且離心率為
(a>b>0)的左、右焦點分別為F1,F2,且離心率為![]() ,M為橢圓上任意一點,當∠F1MF2=90°時,△F1MF2的面積為1.
,M為橢圓上任意一點,當∠F1MF2=90°時,△F1MF2的面積為1.
(Ⅰ)求橢圓C的方程;
(Ⅱ)已知點A是橢圓C上異于橢圓頂點的一點,延長直線AF1,AF2分別與橢圓交于點B,D,設直線BD的斜率為k1,直線OA的斜率為k2,求證:k1·k2等于定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,△ABC為正三角形,AB⊥AD,AC⊥CD,PC= ![]() AC,平面PAC⊥平面ABCD.
AC,平面PAC⊥平面ABCD. 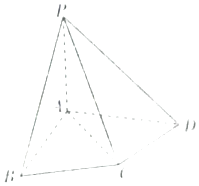
(1)點E在棱PC上,試確定點E的位置,使得PD⊥平面ABE;
(2)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校數學課外興趣小組為研究數學成績是否與性別有關,先統計本校高三年級每個學生一學期數學成績平均分(采用百分制),剔除平均分在40分以下的學生后,共有男生300名,女生200名.現采用分層抽樣的方法,從中抽取了100名學生,按性別分為兩組,并將兩組學生成績分為6組,得到如下所示頻數分布表.

(1)估計男、女生各自的平均分(同一組數據用該組區間中點值作代表),從計算結果看,數學成績與性別是否有關;
(2)規定80分以上為優分(含80分),請你根據已知條件作出2×2列聯表,并判斷是否有90%以上的把握認為“數學成績與性別有關”.

附表及公式:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一商場對每天進店人數和商品銷售件數進行了統計對比,得到如下表格:

其中=1,2,3,4,5,6,7.
(1)以每天進店人數為橫軸,每天商品銷售件數為縱軸,畫出散點圖;
(2)求線性回歸方程;(結果保留到小數點后兩位)
(參考數據:![]() =3 245,
=3 245, ![]() =25,
=25, ![]() =15.43,
=15.43, ![]() =5 075)
=5 075)
(3)預測進店人數為80人時,商品銷售的件數.(結果保留整數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com