
【題目】設f(x)是二次函數,其圖象過點(0,1),且在點(-2,f(-2))處的切線方程為2x+y+3=0
(1)求f(x)的表達式;
(2)求f(x)的圖象與兩坐標軸所圍成圖形的面積;
(3)若直線x=-t(0<t<1)把f(x)的圖象與兩坐標軸所圍成圖形的面積二等分,求t的值.
科目:高中數學 來源: 題型:
【題目】已知A(x1 , f(x1),B(x2 , f(x2))是函數f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)圖象上的任意兩點,且初相φ的終邊經過點P(1,﹣
<φ<0)圖象上的任意兩點,且初相φ的終邊經過點P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4時,|x1﹣x2|的最小值為
),若|f(x1)﹣f(x2)|=4時,|x1﹣x2|的最小值為 ![]() . (Ⅰ)求函數f(x)的解析式;
. (Ⅰ)求函數f(x)的解析式;
(Ⅱ)當x∈[0, ![]() ]時,求函數f(x)的單調遞增區間;
]時,求函數f(x)的單調遞增區間;
(Ⅲ)當x∈[0, ![]() ]時,不等式mf(x)+2m≥f(x)恒成立,求實數m的取值范圍.
]時,不等式mf(x)+2m≥f(x)恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為一簡單組合體,其底面ABCD為正方形,棱PD與EC均垂直于底面ABCD,PD=2EC,N為PB的中點,求證: 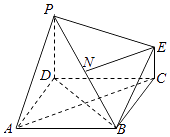
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點Pn(an , bn)滿足an+1=an·bn+1 , bn+1=(n∈N*)且點P1的坐標為(1,-1).
(1)求過點P1 , P2的直線l的方程;
(2)試用數學歸納法證明:對于n∈N* , 點Pn都在(1)中的直線l上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x+2﹣x . (Ⅰ)試寫出這個函數的性質(不少于3條,不必說明理由),并作出圖象;
(Ⅱ)設函數g(x)=4x+4﹣x﹣af(x),求這個函數的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,其中 n 為正整數.
,其中 n 為正整數.
(1)求f(1),f(2),f(3) 的值;
(2)猜想滿足不等式 f(n)<0 的正整數 n 的范圍,并用數學歸納法證明你的猜想.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果命題 p(n) 對 n=k 成立,那么它對 n=k+2 也成立,又若 p(n) 對 n=2 成立,則下列結論正確的是( )
A.p(n) 對所有自然數 n 成立
B.p(n) 對所有正偶數 n 成立
C.p(n) 對所有正奇數 n 成立
D.p(n) 對所有大于1的自然數 n 成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數z=lg(m2﹣2m﹣2)+(m2+3m+2)i,根據以下條件分別求實數m的值或范圍.
(1)z是純虛數;
(2)z對應的點在復平面的第二象限.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com