【答案】
分析:(1)建立空間直角坐標系,分別求出兩條直線所在的向量,進而利用向量的有關運算求出空間向量的夾角,再轉化為兩條異面直線的夾角.
(2)求出平面的法向量以及平面的一條斜線所在的向量,再求出斜線所在的向量在法向量上射影,進而得到答案.
(3)設F(x,0,0),由E(0,1,2),可求出向量
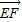
,則
為平面A
1BD的一個法向量,由此構造方程,求出x值,即可得到F點的位置.
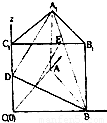
解答:解:(1)如圖建立空間直角坐標系,則B(2,0,0),D(0,0,1),A
1(0,2,2),A(0,2,0),
所以
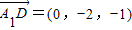
,
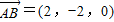
,
所以cos<A
1D,AB>=|

|=
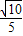
.
所以異面直線A
1D與AB所成角的余弦值為

.
(2)由(1)可得:
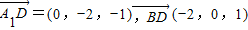
,
設平面A
1DB的法向量為
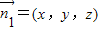
,
則
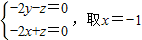
所以可得:
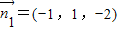
,
又因為
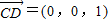
,
所以cos<n
1,
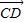
>=

=
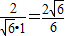
,
所以d=
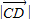
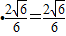
.
所以點C到平面A
1BD的距離

.
(3)存在F為AC的中點,使EF⊥平面A
1BD
設F(0,y,0),由E(1,0,2)得
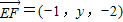
若EF⊥平面A
1BD,則
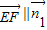
由
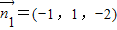
得y=1,
∴F為AC的中點
∴存在F為AC的中點,使EF⊥平面A
1BD
點評:本題考查的知識點是利用空間向量夾角空間夾角與空間距離等問題,并且考查由三視圖還原實物圖,以及基本運算能力.


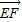 ,則
,則 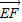 為平面A1BD的一個法向量,由此構造方程,求出x值,即可得到F點的位置.
為平面A1BD的一個法向量,由此構造方程,求出x值,即可得到F點的位置.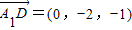 ,
,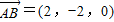 ,
, |=
|=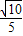 .
.
 .
.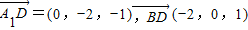 ,
,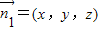 ,
,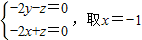
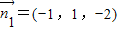 ,
,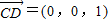 ,
,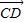 >=
>= =
=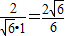 ,
,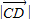
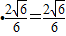 .
. .
.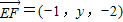
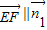 由
由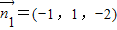 得y=1,
得y=1,

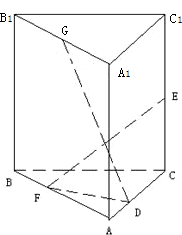
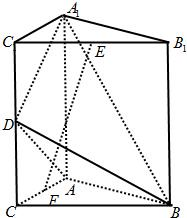 如圖,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分別為棱C1C、B1C1的中點.
如圖,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分別為棱C1C、B1C1的中點. 直三棱柱A1B1C1-ABC的三視圖如圖所示,D、E分別為棱CC1和B1C1的中點.
直三棱柱A1B1C1-ABC的三視圖如圖所示,D、E分別為棱CC1和B1C1的中點.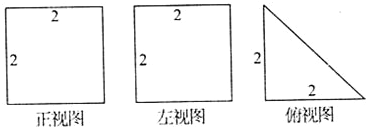
 如圖,在直三棱柱A1B1C1-ABC中,∠BAC=
如圖,在直三棱柱A1B1C1-ABC中,∠BAC= 如圖,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分別為棱C1C、B1C1的中點.
如圖,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分別為棱C1C、B1C1的中點.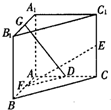 如圖,在直三棱柱A1B1C1-ABC中,∠BAC=
如圖,在直三棱柱A1B1C1-ABC中,∠BAC=