
【題目】一片森林原面積為![]() .計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的
.計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的![]() .已知到今年為止,森林剩余面積為原面積的
.已知到今年為止,森林剩余面積為原面積的![]() .
.
(1)求每年砍伐面積的百分比;
(2)到今年為止,該森林已砍伐了多少年?
(3)為保護生態環境,今后最多還能砍伐多少年?
【答案】(1)![]() ;(2)到今年為止,已砍伐了5年;(3)今后最多還能砍伐15年.
;(2)到今年為止,已砍伐了5年;(3)今后最多還能砍伐15年.
【解析】試題分析:(1)根據每年砍伐面積的百分比相等,當砍伐到面積的一半時,所用時間是10年,設每年砍伐面積的百分比為x 可建立方程,解之即可得到每年砍伐面積的百分比;
(2)設經過m年剩余面積為原來的![]() .根據題意:到今年為止,森林剩余面積為原來的
.根據題意:到今年為止,森林剩余面積為原來的![]() .可列出關于m的等式,解之即可;
.可列出關于m的等式,解之即可;
(3)根據題意設從今年開始,以后砍了n年,再求出砍伐n年后剩余面積,由題意,建立關于n的不等關系,利用一些不等關系即可求得今后最多還能砍伐多少年.
解:(1)設每年砍伐面積的百分比為x ( 0<x<1).則![]() ,
,
即![]() ,解得
,解得![]()
(2)設經過m年剩余面積為原來的![]() ,則
,則![]() ,
,
即![]() ,
,![]() ,解得m=5
,解得m=5
故到今年為止,已砍伐了5年.
(3)設從今年開始,以后砍了n年,則n年后剩余面積為![]()
令![]() ≥
≥![]() ,即(1﹣x)n≥
,即(1﹣x)n≥![]() ,
,![]() ≥
≥![]() ,
,![]() ≤
≤![]() ,
,
解得n≤15
故今后最多還能砍伐15年.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學名著《續古摘奇算法》(楊輝)一書中有關于三階幻方的問題:將1,2,3,4,5,6,7,8,9分別填入![]() 的方格中,使得每一行,每一列及對角線上的三個數的和都相等,我們規定:只要兩個幻方的對應位置(如每行第一列的方格)中的數字不全相同,就稱為不同的幻方,那么所有不同的三階幻方的個數是( )
的方格中,使得每一行,每一列及對角線上的三個數的和都相等,我們規定:只要兩個幻方的對應位置(如每行第一列的方格)中的數字不全相同,就稱為不同的幻方,那么所有不同的三階幻方的個數是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一批產品需要進行質量檢驗,檢驗方案是:先從這批產品中任取4件作檢驗,這4件產品中優質品的件數記為n.如果n=3,再從這批產品中任取4件作檢驗,若都為優質品,則這批產品通過檢驗;如果n=4,再從這批產品中任取1件作檢驗,若為優質品,則這批產品通過檢驗;其他情況下,這批產品都不能通過檢驗.
假設這批產品的優質品率為50%,即取出的產品是優質品的概率都為![]() ,且各件產品是否為優質品相互獨立.
,且各件產品是否為優質品相互獨立.
(1)求這批產品通過檢驗的概率;
(2)已知每件產品檢驗費用為100元,凡抽取的每件產品都需要檢驗,對這批產品作質量檢驗所需的費用記為X(單位:元),求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.
如圖,在陽馬![]() 中,側棱
中,側棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 為
為![]() 中點,點
中點,點![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,連接
,連接![]() ,
, ![]() .
.
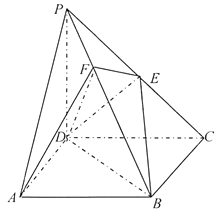
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)試判斷四面體![]() 是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示2×2方格,在每一個方格中填入一個數字,數字可以是1、2、3、4中的任何一個,允許重復.若填入A方格的數字大于B方格的數字,則不同的填法共有( )
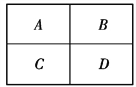
A. 192種 B. 128種 C. 96種 D. 12種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,且
,且![]() .
.
(1)求函數![]() 在
在![]() 上的單調區間,并給以證明;
上的單調區間,并給以證明;
(2)設關于![]() 的方程
的方程![]() 的兩根為
的兩根為![]() ,試問是否存在實數
,試問是否存在實數![]() ,使得不等式
,使得不等式![]() 對任意的
對任意的![]() 及
及![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙同學參加學校“一站到底”闖關活動,活動規則:①依次闖關過程中,若闖關成功則繼續答題;若沒通關則被淘汰;②每人最多闖3關;③闖第一關得10分,闖第二關得20分,闖第三關得30分,一關都沒過則沒有得分.已知甲每次闖關成功的概率為![]() ,乙每次闖關成功的概率為
,乙每次闖關成功的概率為![]() .
.
(Ⅰ)設乙的得分總數為![]() ,求
,求![]() 得分布列和數學期望;
得分布列和數學期望;
(Ⅱ)求甲恰好比乙多30分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】河南多地遭遇跨年霾,很多學校調整元旦放假時間,提前放假讓學生們在家里躲霾,鄭州市根據《鄭州市人民政府辦公廳關于將重污染天氣黃色預警升級為紅色預警的通知》.自12月29日12時將黃色預警升級為紅色預警,12月30日0時啟動I級響應,明確要求:“幼兒園、中小學等教育機構停課,停課不停學”,學生和家長對停課這一舉措褒貶不一,有為了健康贊成的,有怕耽誤學習不贊成的.某調查機構為了了解公眾對該舉措的態度,隨機調查采訪了50人,將調查情況整理匯總成下表:
年齡(歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)請補全被調查人員年齡的頻率分布直方圖;
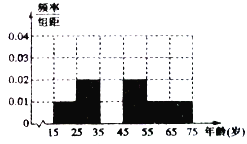
(2)若從年齡在![]() 的被調查者中分別隨機選取一人進行追蹤調查,求這兩人都贊成“停課”這一舉措的概率.
的被調查者中分別隨機選取一人進行追蹤調查,求這兩人都贊成“停課”這一舉措的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com