
【題目】設(shè)拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,過點(diǎn)
,過點(diǎn)![]() 作垂直于
作垂直于![]() 軸的直線與拋物線交于
軸的直線與拋物線交于![]() ,
,![]() 兩點(diǎn),且以線段
兩點(diǎn),且以線段![]() 為直徑的圓過點(diǎn)
為直徑的圓過點(diǎn)![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 為曲線
為曲線![]() :
:![]() 上的動(dòng)點(diǎn),求
上的動(dòng)點(diǎn),求![]() 面積的最小值.
面積的最小值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)由于![]() 與
與![]() 軸垂直,因此
軸垂直,因此![]() 就是圓心,
就是圓心,![]() 的長(zhǎng)是拋物線的通徑長(zhǎng)
的長(zhǎng)是拋物線的通徑長(zhǎng)![]() ,從而易求得
,從而易求得![]() ;
;
(2)點(diǎn)![]() ,
,![]() ,把直線
,把直線![]() 方程與拋物線方程聯(lián)立,消去
方程與拋物線方程聯(lián)立,消去![]() 得
得![]() 的一元二次方程,由韋達(dá)定理得
的一元二次方程,由韋達(dá)定理得![]() ,從而可得
,從而可得![]() ,設(shè)動(dòng)點(diǎn)
,設(shè)動(dòng)點(diǎn)![]() ,求出
,求出![]() 到直線
到直線![]() 的距離,利用基本不等式可求得它的最小值,從而得三角形面積的最小值.
的距離,利用基本不等式可求得它的最小值,從而得三角形面積的最小值.
(1)由題意得,圓的半徑![]() ,解得:
,解得:![]()
故拋物線的方程為![]() .
.
(2)設(shè)點(diǎn)![]() ,
,![]() ,由直線
,由直線![]() 過拋物線的焦點(diǎn)
過拋物線的焦點(diǎn)![]() ,
,
聯(lián)立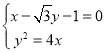 得
得![]() ,
,
故![]() ,所以
,所以![]()
由點(diǎn)![]() 為曲線
為曲線![]() 上的動(dòng)點(diǎn),設(shè)點(diǎn)
上的動(dòng)點(diǎn),設(shè)點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 到直線
到直線![]() 的距離
的距離
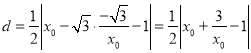 ,
,
由![]() ,故
,故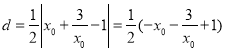
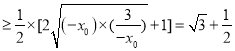
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí),取等號(hào),所以
時(shí),取等號(hào),所以![]() ,
,
∴![]()
![]() ,
,
故![]() 面積的最小值為
面積的最小值為![]() .
.


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是邊長(zhǎng)為2的正方形,
是邊長(zhǎng)為2的正方形,![]() 為
為![]() 的中點(diǎn),以
的中點(diǎn),以![]() 為折痕把
為折痕把![]() 折起,使點(diǎn)
折起,使點(diǎn)![]() 到達(dá)點(diǎn)
到達(dá)點(diǎn)![]() 的位置,且
的位置,且![]() .
.
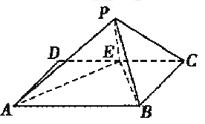
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】筒車是我國古代發(fā)明的一種水利灌溉工具,明朝科學(xué)家徐光啟在《農(nóng)政全書》中用圖畫描繪了筒車的工作原理(如圖1).因其經(jīng)濟(jì)又環(huán)保,至今還在農(nóng)業(yè)生產(chǎn)中得到使用(如圖2).假定在水流量穩(wěn)定的情況下,筒車上的每一個(gè)盛水筒都做勻速圓周運(yùn)動(dòng).因筒車上盛水筒的運(yùn)動(dòng)具有周期性,可以考慮利用三角函數(shù)模型刻畫盛水筒(視為質(zhì)點(diǎn))的運(yùn)動(dòng)規(guī)律.將筒車抽象為一個(gè)幾何圖形,建立直角坐標(biāo)系(如圖3).設(shè)經(jīng)過t秒后,筒車上的某個(gè)盛水筒![]() 從點(diǎn)P0運(yùn)動(dòng)到點(diǎn)P.由筒車的工作原理可知,這個(gè)盛水筒距離水面的高度H(單位:
從點(diǎn)P0運(yùn)動(dòng)到點(diǎn)P.由筒車的工作原理可知,這個(gè)盛水筒距離水面的高度H(單位: ![]() ),由以下量所決定:筒車轉(zhuǎn)輪的中心O到水面的距離h,筒車的半徑r,筒車轉(zhuǎn)動(dòng)的角速度ω(單位:
),由以下量所決定:筒車轉(zhuǎn)輪的中心O到水面的距離h,筒車的半徑r,筒車轉(zhuǎn)動(dòng)的角速度ω(單位: ![]() ),盛水筒的初始位置P0以及所經(jīng)過的時(shí)間t(單位:
),盛水筒的初始位置P0以及所經(jīng)過的時(shí)間t(單位:![]() ).已知r=3
).已知r=3![]() ,h=2
,h=2![]() ,筒車每分鐘轉(zhuǎn)動(dòng)(按逆時(shí)針方向)1.5圈, 點(diǎn)P0距離水面的高度為3.5
,筒車每分鐘轉(zhuǎn)動(dòng)(按逆時(shí)針方向)1.5圈, 點(diǎn)P0距離水面的高度為3.5![]() ,若盛水筒M從點(diǎn)P0開始計(jì)算時(shí)間,則至少需要經(jīng)過_______
,若盛水筒M從點(diǎn)P0開始計(jì)算時(shí)間,則至少需要經(jīng)過_______![]() 就可到達(dá)最高點(diǎn);若將點(diǎn)
就可到達(dá)最高點(diǎn);若將點(diǎn)![]() 距離水面的高度
距離水面的高度![]() 表示為時(shí)間
表示為時(shí)間![]() 的函數(shù),則此函數(shù)表達(dá)式為_________.
的函數(shù),則此函數(shù)表達(dá)式為_________.



圖1 圖2 圖3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某藝術(shù)團(tuán)組織的“微視頻展示”活動(dòng)中,該團(tuán)體將從微視頻的“點(diǎn)贊量”和“專家評(píng)分”兩個(gè)角度來進(jìn)行評(píng)優(yōu).若A視頻的“點(diǎn)贊量”和“專家評(píng)分”中至少有一項(xiàng)高于B視頻,則稱A視頻不亞于B視頻.已知共有5部微視頻展,如果某微視頻不亞于其他4部視頻,就稱此視頻為優(yōu)秀視頻.那么在這5部微視頻中,最多可能有_______個(gè)優(yōu)秀視頻.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)A,B分別是雙曲線![]() 的左右頂點(diǎn),設(shè)過
的左右頂點(diǎn),設(shè)過![]() 的直線PA,PB與雙曲線分別交于點(diǎn)M,N,直線MN交x軸于點(diǎn)Q,過Q的直線交雙曲線的于S,T兩點(diǎn),且
的直線PA,PB與雙曲線分別交于點(diǎn)M,N,直線MN交x軸于點(diǎn)Q,過Q的直線交雙曲線的于S,T兩點(diǎn),且![]() ,則
,則![]() 的面積( )
的面積( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() ,在圓
,在圓![]() :
:![]() 上任取一點(diǎn)
上任取一點(diǎn)![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點(diǎn)
于點(diǎn)![]() .(如圖).
.(如圖).
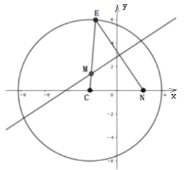
(1)求點(diǎn)![]() 的軌跡方程
的軌跡方程![]() ;
;
(2)若過點(diǎn)![]() 的動(dòng)直線
的動(dòng)直線![]() 與(1)中的軌跡
與(1)中的軌跡![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn).問:平面內(nèi)是否存在異于點(diǎn)
兩點(diǎn).問:平面內(nèi)是否存在異于點(diǎn)![]() 的定點(diǎn)
的定點(diǎn)![]() ,使得
,使得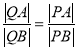 恒成立?試證明你的結(jié)論.
恒成立?試證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C經(jīng)過A(5,3),B(4,4)兩點(diǎn),且圓心在x軸上.
(1)求圓C的標(biāo)準(zhǔn)方程;
(2)若直線l過點(diǎn)(5,2),且被圓C所截得的弦長(zhǎng)為6,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,以原點(diǎn)0為極點(diǎn),
,以原點(diǎn)0為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)若曲線![]() 方程中的參數(shù)是
方程中的參數(shù)是![]() ,且
,且![]() 與
與![]() 有且只有一個(gè)公共點(diǎn),求
有且只有一個(gè)公共點(diǎn),求![]() 的普通方程;
的普通方程;
(2)已知點(diǎn)![]() ,若曲線
,若曲線![]() 方程中的參數(shù)是
方程中的參數(shù)是![]() ,
,![]() ,且
,且![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩個(gè)不同點(diǎn),求
兩個(gè)不同點(diǎn),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 與
與![]() 的圖像相交于點(diǎn)
的圖像相交于點(diǎn)![]() ,
,![]() 兩點(diǎn),若動(dòng)點(diǎn)
兩點(diǎn),若動(dòng)點(diǎn)![]() 滿足
滿足![]() ,則點(diǎn)
,則點(diǎn)![]() 的軌跡方程是______.
的軌跡方程是______.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com