【題目】在平面直角坐標系
中，二次函數
的圖象與坐標軸的交點都在圓
上．
（1）求圓的方程；
（2）直線
交圓于
、
兩點，且
，求
．
【答案】（1）
；（2）
.
【解析】
（1）求出二次函數
的圖象與坐標軸的三個交點坐標，可知圓心在直線
上，可設圓心坐標為
，利用圓心到二次函數與
軸的交點以及與
軸的一個交點的距離相等列等式求出
的值，進而可得出圓
的方程；
（2）設點
、
，將直線
的方程與圓的方程聯立，列出韋達定理，利用向量數量積的坐標運算結合條件
求出
的值，由此可得出直線的方程，并計算出圓心到直線的距離，利用勾股定理可計算出
.
（1）令
，得
．所以拋物線與軸交點為
．
令
，得
，解得
.
所以拋物線與軸的交點為
，
．
設圓心坐標為
，則有
，解得
．
所以圓的半徑
，所以圓的方程為；
（2）設，，
聯立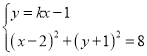
，消去并整理得
．
所以
，
，
，
由題設可得
，解得
，所以
，即
．
又圓心到直線的距離
，所以
．
科目：高中數學 來源： 題型：
【題目】橢圓
的中心在原點，焦點在
軸上，離心率
，它的一個頂點恰好是拋物線
的焦點.
（1）求橢圓
的標準方程；
（2）過坐標原點的直線
交橢圓于
兩點，
在第一象限，
軸，垂足為
，連接
延長交橢圓于點
.
①求證：
；
②求
面積最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司在招聘員工時，要進行筆試，面試和實習三個過程．筆試設置了3個題，每一個題答對得5分，否則得0分．面試則要求應聘者回答3個問題，每一個問題答對得5分，否則得0分．并且規定在筆試中至少得到10分，才有資格參加面試，而筆試和面試得分之和至少為25分，才有實習的機會．現有甲去該公司應聘，假設甲答對筆試中的每一個題的概率為
，答對面試中的每一個問題的概率為
．
（1）求甲獲得實習機會的概率；
（2）設甲在去應聘過程中的所得分數為隨機變量
，求的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）若
時，求函數
在點
處的切線方程；
（2）若函數在
時取得極值，當
時，求使得
恒成立的實數
的取值范圍；
（3）若函數在區間
上單調遞減，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解今年某校高三畢業班準備報考飛行員學生的體重情況，將所得的數據整理后，畫出了頻率分布直方圖（如圖），已知圖中從左到右的前3個小組的頻率之比為1：2：3，其中第2小組的頻數為12．
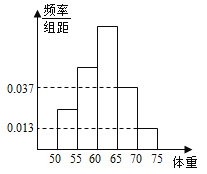
（1）求該校報考飛行員的總人數；
（2）以這所學校的樣本數據來估計全省的總體數據，若從全省報考飛行員的同學中（人數很多）任選三人，設
表示體重超過60公斤的學生人數，求的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2+y2+2x﹣2y+1＝0和拋物線E：y2＝2px（p＞0），圓C與拋物線E的準線交于M、N兩點，△MNF的面積為p，其中F是E的焦點．
（1）求拋物線E的方程；
（2）不過原點O的動直線l交該拋物線于A，B兩點，且滿足OA⊥OB，設點Q為圓C上任意一動點，求當動點Q到直線l的距離最大時直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學數學老師分別用兩種不同教學方式對入學數學平均分和優秀率都相同的甲、乙兩個高一新班（人數均為
人）進行教學（兩班的學生學習數學勤奮程度和自覺性一致），數學期終考試成績莖葉圖如下：
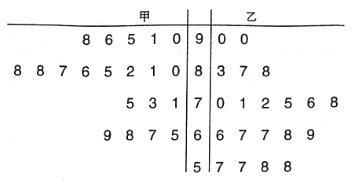
（1）現從乙班數學成績不低于
分的同學中隨機抽取兩名同學，求至少有一名成績為
分的同學被抽中的概率；
（2）學校規定：成績不低于
分的優秀，請填寫下面的
聯表，并判斷有多大把握認為“成績優秀與教學方式有關”．
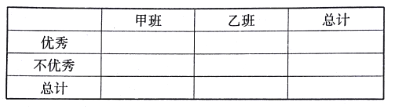
附：參考公式及數據
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
