【題目】如圖，在四面體A-BCD中，已知平面
平面BCD，
為正三角形，
為等腰直角三角形，其中C為直角頂點，E，F分別為校AC，AD的中點.
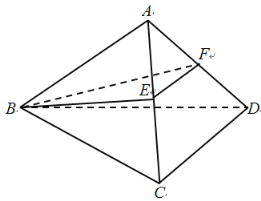
（1）求證：
平面BEF；
（2）求證：
平面ACD.
課堂全解字詞句段篇章系列答案
步步高口算題卡系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】2020年新冠肺炎疫情暴發(fā)以來，中國政府迅速采取最全面、最嚴(yán)格、最徹底的防控舉措，堅決遏制疫情蔓延勢頭，努力把疫情影響降到最低，為全世界抗擊新冠肺炎疫情做岀了貢獻．為普及防治新冠肺炎的相關(guān)知識，某高中學(xué)校開展了線上新冠肺炎防控知識競答活動，現(xiàn)從大批參與者中隨機抽取200名幸運者，他們的得分（滿分100分）數(shù)據(jù)統(tǒng)計結(jié)果如圖：
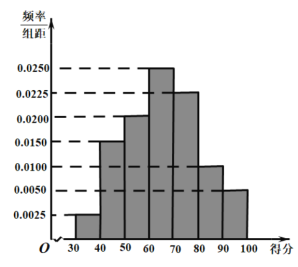
（1）若此次知識競答得分
整體服從正態(tài)分布，用樣本來估計總體，設(shè)
，
分別為這200名幸運者得分的平均值和標(biāo)準(zhǔn)差（同一組數(shù)據(jù)用該區(qū)間中點值代替），求，的值（，的值四舍五入取整數(shù)），并計算
；
（2）在（1）的條件下，為感謝大家積極參與這次活動，對參與此次知識競答的幸運者制定如下獎勵方案：得分低于的獲得1次抽獎機會，得分不低于的獲得2次抽獎機會．假定每次抽獎中，抽到18元紅包的概率為
，抽到36元紅包的概率為
．已知高三某同學(xué)是這次活動中的幸運者，記
為該同學(xué)在抽獎中獲得紅包的總金額，求的分布列和數(shù)學(xué)期望，并估算舉辦此次活動所需要抽獎紅包的總金額．
參考數(shù)據(jù)：
；
；
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左右頂點分別為A，B，離心率為
，長軸長為4，動點S在C上位于x軸上方，直線
與直線
，分別交于M，N兩點.
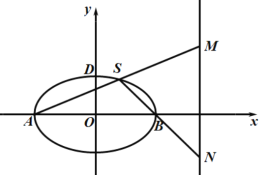
（1）求橢圓C的方程
（2）求|MN|的最小值
（3）當(dāng)
最小時，在橢圓C上是否存在這樣的點T，使△TSB面積為
？若存在，請確定點T的個數(shù)；若不存在，請說明理由
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某市旅游管理部門為提升該市26個旅游景點的服務(wù)質(zhì)量，對該市26個旅游景點的交通、安全、環(huán)保、衛(wèi)生、管理五項指標(biāo)進行評分，每項評分最低分0分，最高分100分，每個景點總分為這五項得分之和，根據(jù)考核評分結(jié)果，繪制交通得分與安全得分散點圖、交通得分與景點總分散點圖如下：
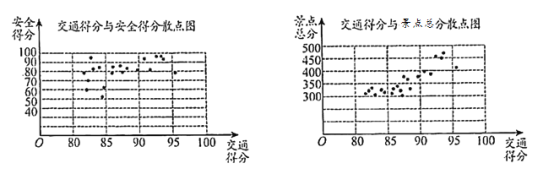
請根據(jù)圖中所提供的信息，完成下列問題：
（I）若從交通得分前6名的景點中任取2個，求其安全得分都大于90分的概率；
（II）若從景點總分排名前6名的景點中任取3個，記安全得分不大于90分的景點個數(shù)為
，求隨機變量的分布列和數(shù)學(xué)期望；
（III）記該市26個景點的交通平均得分為
安全平均得分為
，寫出
和的大小關(guān)系？（只寫出結(jié)果）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖．正四面體ABCD的頂點A，B，C分別在兩兩垂直的三條射線OX，OY，OZ上，則在下列命題中，錯誤的為（ ）
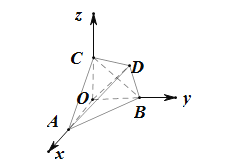
A.O﹣ABC是正三棱錐B.二面角D﹣OB﹣A的平面角為
C.直線AD與直線OB所成角為
D.直線OD⊥平面ABC
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在空間直角坐標(biāo)系
中，已知正四棱錐P-ABCD的所有棱長均為6，正方形ABCD的中心為坐標(biāo)原點O，AD，BC平行于x軸，AB、CD平行于y軸，頂點P在z軸的正半軸上，點M、N分別在PA，BD上，且
.
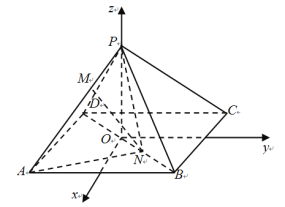
（1）若
，求直線MN與PC所成角的大小；
（2）若二面角A-PN-D的平面角的余弦值為
，求λ的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在平面直角坐標(biāo)系xOy中，橢圓
的右焦點、右頂點分別為F，A，過原點的直線與橢圓C交于點P、Q（點P在第一象限內(nèi)），連結(jié)PA，QF．若
，
的面積是
面積的3倍．
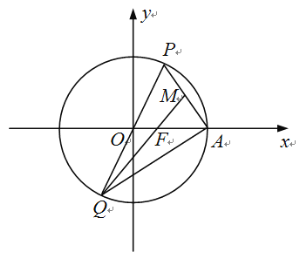
（1）求橢圓C的標(biāo)準(zhǔn)方程；
（2）已知M為線段PA的中點，連結(jié)QA，QM．
①求證：Q，F，M三點共線；
②記直線QP，QM，QA的斜率分別為
，
，
，若
，求
的面積．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)橢圓
的右焦點為
，以原點
為圓心，短半軸長為半徑的圓恰好經(jīng)過橢圓
的兩焦點，且該圓截直線
所得的弦長為
.
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）過定點
的直線交橢圓于兩點
、
，橢圓上的點
滿足
，試求
的面積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
滿足
．
（1）求數(shù)列的通項公式；
（2）設(shè)
，數(shù)列
的前
項和為
，求；
（3）設(shè)
，問：是否存在非零整數(shù)
，使數(shù)列
為遞增數(shù)列？若存在，求出的值；若不存在，請說明理由．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
