
【題目】已知函數![]() ,
, ![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)當![]() 時,令
時,令![]() ,其導函數為
,其導函數為![]() ,設
,設![]() 是函數
是函數![]() 的兩個零點,判斷
的兩個零點,判斷![]() 是否為
是否為![]() 的零點?并說明理由.
的零點?并說明理由.
【答案】(1)見解析;(2)見解析
【解析】試題分析:(Ⅰ)先求導,再分類討論,根據導數和函數單調性的關系即可求出,
(Ⅱ)由(Ⅰ)知,g(x)=x2﹣2lnx﹣x,x1,x2是函數g(x)的兩個零點,不妨設0<x1<x2,可得x12﹣2lnx1﹣x1=0,x22﹣2lnx2﹣x2=0,兩式相減化簡可得x1+x2﹣1=![]() ,再對g(x)求導,判斷
,再對g(x)求導,判斷![]() 的符號即可證明
的符號即可證明
試題解析:
(1)依題意知函數![]() 的定義域為
的定義域為![]() ,且
,且![]() .
.
①當![]() 時,
時, ![]() ,所以
,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
②當![]() 時,由
時,由![]() 得:
得: ![]() ,
,
則當![]() 時
時![]() ;當
;當![]() 時
時![]() .
.
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)![]() 不是導函數
不是導函數![]() 的零點.
的零點.
證明如下:由(Ⅰ)知函數![]() .
.
∵![]() ,
, ![]() 是函數
是函數![]() 的兩個零點,不妨設
的兩個零點,不妨設![]() ,
,
∴![]() ,兩式相減得:
,兩式相減得: ![]()
即: ![]()
又![]() .
.
則![]()
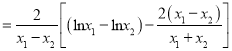 .
.
設![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,
, 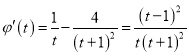 .
.
又![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是増函數,
上是増函數,
則![]() ,即當
,即當![]() 時,
時, ![]() ,
,
從而![]() ,
,
又![]() 所以
所以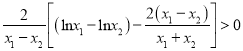 ,
,
故![]() ,所以
,所以![]() 不是導函數
不是導函數![]() 的零點.
的零點.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的維修費用
(年)和所支出的維修費用![]() (萬元)有如下統(tǒng)計資料:
(萬元)有如下統(tǒng)計資料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由資料知, ![]() 對
對![]() 呈線性相關關系,試求:
呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少?
參考公式:回歸直線方程: ![]() .其中
.其中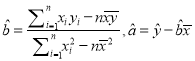
(注: ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2+bx+c(a,b,c∈R),若x=﹣1為函數y=f(x)ex的一個極值點,則下列圖象不可能為y=f(x)的圖象是( )
A. 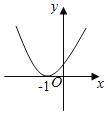 B.
B. 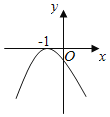
C. 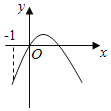 D.
D. 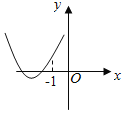
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過函數性質的學習,我們知道:“函數![]() 的圖象關于
的圖象關于![]() 軸成軸對稱圖形”的充要條件是“
軸成軸對稱圖形”的充要條件是“![]() 為偶函數”.
為偶函數”.
(1)若![]() 為偶函數,且當
為偶函數,且當![]() 時,
時,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某數學學習小組針對上述結論進行探究,得到一個真命題:“函數![]() 的圖象關于直線
的圖象關于直線![]() 成軸對稱圖形”的充要條件是“
成軸對稱圖形”的充要條件是“![]() 為偶函數”.若函數
為偶函數”.若函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,且當
對稱,且當![]() 時,
時,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】右圖是一個幾何體的平面展開圖,其中ABCD為
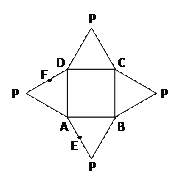
正方形, E、F分別為PA、PD的中點,在此幾何體中,
給出下面四個結論:
①直線BE與直線CF異面;②直線BE與直線AF異面;
③直線EF//平面PBC; ④平面BCE⊥平面PAD.
其中正確結論的個數是
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為D={x|x≠0},且滿足對于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明你的結論;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函數,求x的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com