【題目】血藥濃度（Plasma Concentration）是指藥物吸收后在血漿內的總濃度. 藥物在人體內發揮治療作用時，該藥物的血藥濃度應介于最低有效濃度和最低中毒濃度之間.已知成人單次服用1單位某藥物后，體內血藥濃度及相關信息如圖所示：
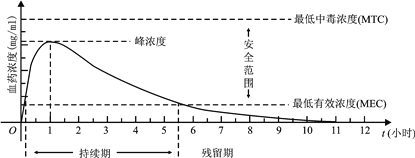
根據圖中提供的信息，下列關于成人使用該藥物的說法中，不正確的個數是
①首次服用該藥物1單位約10分鐘后，藥物發揮治療作用
②每次服用該藥物1單位，兩次服藥間隔小于2小時，一定會產生藥物中毒
③每間隔5.5小時服用該藥物1單位，可使藥物持續發揮治療作用
④首次服用該藥物1單位3小時后，再次服用該藥物1單位，不會發生藥物中毒
A. 1個 B. 2個 C. 3個 D. 4個
【答案】A
【解析】對于①,由圖象中最低有效濃度與體內血液濃度的第一個交點坐標可知正確;對于②,當第二個單位的藥服用一小時時的血液濃度為峰濃度,此時第一個單位的藥物已服用三小時,此時血液濃度必超過最低中毒濃度,因此一定會產生藥物中毒,正確;對于③,由圖知, 每間隔5.5小時服用該藥物,血液濃度都在最低有效濃度之上,正確;對于④, 首次服用該藥物1單位3小時后，再次服用該藥物1單位，過一個小時之后,第二個單位的藥物達到峰濃度,兩個單位的藥物的血液濃度仍超過最低中毒濃度,故錯誤;綜上可知,應選A.
點睛:本題考查根據圖象識別信息的能力,屬于中檔題目.觀察圖象提供的信息,準確的獲取信息是解題關鍵.由圖象可得函數先增后減,在t=1時取到極大值,在血液濃度所對應的值超過最低中毒濃度時,會發生藥物中毒,因此兩次服藥的間隔不能太小,需要看是否有兩次藥效之和超過最低值.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，過
的左焦點
的直線
，直線
被圓
：
截得的弦長為
.
（Ⅰ）求橢圓的方程；
（Ⅱ）設的右焦點為
，在圓上是否存在點
，滿足
，若存在，指出有幾個這樣的點（不必求出點的坐標）；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
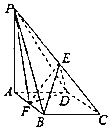
【題目】如圖：在四棱錐P﹣ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=3，PA⊥底面ABCD，E是PC中點，F是AB中點．
（Ⅰ）求證：BE∥平面PDF；
（Ⅱ）求直線PD與平面PFB所成角的正切值；
（Ⅲ）求三棱錐P﹣DEF的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）=log 
為奇函數，a為常數，
（1）求a的值；
（2）證明f（x）在區間（1，+∞）上單調遞增；
（3）若x∈[3，4]，不等式f（x）＞（ 
）x+m恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2﹣4x+a+3，a∈R．
（1）若函數y=f（x）的圖象與x軸無交點，求a的取值范圍；
（2）若函數y=f（x）在[﹣1，1]上存在零點，求a的取值范圍；
（3）設函數g（x）=bx+5﹣2b，b∈R．當a=0時，若對任意的x1∈[1，4]，總存在x2∈[1，4]，使得f（x1）=g（x2），求b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中,已知曲線
的參數方程為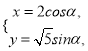
(
為參數),以直角坐標系原點
為極點, 
軸的正半軸為極軸建立極坐標系,直線
的極坐標方程為
.
(Ⅰ)求曲線
的普通方程與直線
的直角坐標方程；
(Ⅱ)設點
為曲線
上的動點,求點
到直線
距離的最大值及其對應的點
的直角坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）已知拋物線
的頂點在坐標原點
，對稱軸為
軸，焦點為
,拋物線上一點
的橫坐標為
，且
.
（Ⅰ）求此拋物線的方程；
（Ⅱ）過點
做直線
交拋物線
于
兩點,求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在[﹣1，1]上的奇函數f（x），已知當x∈[﹣1，0]時的解析式f（x）= 
﹣ 
（a∈R）．
（1）寫出f（x）在[0，1]上的解析式；
（2）求f（x）在[0，1]上的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
