
【題目】設A={﹣4,2a﹣1,a2},B={a﹣1,1﹣a,9},已知A∩B={9},求a的值.
【答案】解:∵A={﹣4,2a﹣1,a2},B={a﹣1,1﹣a,9},且A∩B={9},∴9∈A且9∈B,
可得2a﹣1=9或a2=9,解得:a=5或a=±3,
當a=5時,A={﹣4,9,25},B={4,﹣4,9},則有A∩B={﹣4,9},不合題意,故a=5舍去;
當a=3時,A={﹣4,5,9},B={2,﹣2,9},此時A∩B={9},符合題意;
當a=﹣3時,A={﹣4,﹣7,9},B={﹣4,4,9},此時A∩B={﹣4,9},不符合題意,
則a=3
【解析】根據A與B的交集中元素為9,得到9屬于A且屬于B,即可確定出a的值.
【考點精析】關于本題考查的集合的交集運算,需要了解交集的性質:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,則A
,A∩B=B∩A;(2)若A∩B=A,則A![]() B,反之也成立才能得出正確答案.
B,反之也成立才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】如圖,菱形ABCD與正三角形BCE的邊長均為2,它們所在平面互相垂直,FD⊥平面ABCD,且 ![]() .
. 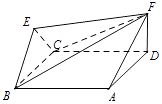
(1)若∠BCD=60°,求證:BC⊥EF;
(2)若∠CBA=60°,求直線AF與平面FBE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題中
① 非零向量![]() 滿足
滿足![]() ,則
,則![]() 的夾角為
的夾角為![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夾角為銳角的充要條件;
的夾角為銳角的充要條件;
③若![]() 則
則![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圓的圓心為O,半徑為1,若![]() ,且
,且![]() ,則向量
,則向量![]() 在向量
在向量![]() 方向上的投影為
方向上的投影為![]() .
.
以上命題正確的是 __________ (注:把你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體是由棱臺![]() 和棱錐
和棱錐![]() 拼接而成的組合體,其底面四邊形
拼接而成的組合體,其底面四邊形![]() 是邊長為
是邊長為![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求證:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
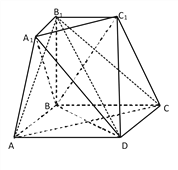
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬;將四個面都為直角三角形的三棱錐稱之為鱉臑.若三棱錐![]() 為鱉臑,
為鱉臑, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,三棱錐
,三棱錐![]() 的四個頂點都在球
的四個頂點都在球![]() 的球面上,則球
的球面上,則球![]() 的表面積為( ).
的表面積為( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4;坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點, ![]() 軸正半軸為極軸的極坐標中,曲線
軸正半軸為極軸的極坐標中,曲線![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程.
的直角坐標方程.
(Ⅱ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知n為正整數,數列{an}滿足an>0, ![]() ,設數列{bn}滿足
,設數列{bn}滿足 ![]()
(1)求證:數列 ![]() 為等比數列;
為等比數列;
(2)若數列{bn}是等差數列,求實數t的值;
(3)若數列{bn}是等差數列,前n項和為Sn , 對任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求滿足條件的所有整數a1的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com