
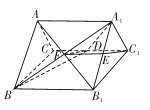
【題目】如圖所示,直三棱柱![]() 中,
中, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 的中點.
的中點.

(1)求證: ![]() 面
面![]() ;
;
(2)若![]() 面
面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)設(shè)![]() 與
與![]() 交于
交于![]() ,連接
,連接![]() ,∵
,∵![]() ,則
,則![]() 與
與![]() 平行且相等.∴四邊形
平行且相等.∴四邊形![]() 為平行四邊形,由線面平行的判定定理可得結(jié)果;(2)以
為平行四邊形,由線面平行的判定定理可得結(jié)果;(2)以![]() 的中點
的中點![]() 為原點,分別以
為原點,分別以![]() 方向為
方向為![]() 軸和
軸和![]() 軸正方向,以
軸正方向,以![]() 方向為
方向為![]() 軸正方向,建立空間直角坐標系,分別求出平面與平面的一個法向量,根據(jù)空間向量夾角余弦公式,可得結(jié)果.
軸正方向,建立空間直角坐標系,分別求出平面與平面的一個法向量,根據(jù)空間向量夾角余弦公式,可得結(jié)果.
試題解析:(1)設(shè)![]() 與
與![]() 交于
交于![]() ,連接
,連接![]() ,
,
∵![]() ,則
,則![]() 與
與![]() 平行且相等.
平行且相等.
∴四邊形![]() 為平行四邊形.
為平行四邊形.
∴![]() ,又
,又![]() 面
面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
(2)以![]() 的中點
的中點![]() 為原點,分別以
為原點,分別以![]() 方向為
方向為![]() 軸和
軸和![]() 軸正方向,以
軸正方向,以![]() 方向為
方向為![]() 軸正方向,建系如圖,設(shè)
軸正方向,建系如圖,設(shè)![]() ,
, ![]() ,則有
,則有
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]()
由![]() 面
面![]() ,則
,則![]() .
.
則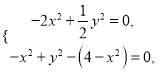 解得
解得![]() .
.
所以面![]() 的法向量為
的法向量為![]() ,
,
又設(shè)面![]() 的法向量為
的法向量為![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,所以
,所以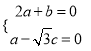 ,令
,令![]() ,
,
則![]() ,
,
∴![]() .
.
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
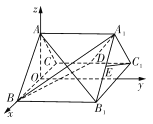
【方法點晴】本題主要考查線面平行的判定定理、利用空間向量求二面角,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關(guān)鍵是設(shè)法在平面內(nèi)找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質(zhì)或者構(gòu)造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質(zhì),即兩平面平行,在其中一平面內(nèi)的直線平行于另一平面. 本題(1)是就是利用方法①證明的.


 考前必練系列答案
考前必練系列答案科目:高中數(shù)學 來源: 題型:
【題目】預(yù)計某地區(qū)明年從年初開始的前 ![]() 個月內(nèi),對某種商品的需求總量
個月內(nèi),對某種商品的需求總量 ![]() (萬件)近似滿足:
(萬件)近似滿足: ![]() ,且
,且 ![]() )
)
(1)寫出明年第 ![]() 個月的需求量
個月的需求量 ![]() (萬件)與月份
(萬件)與月份 ![]() 的函數(shù)關(guān)系式,并求出哪個月份的需求量超過
的函數(shù)關(guān)系式,并求出哪個月份的需求量超過 ![]() 萬件;
萬件;
(2)如果將該商品每月都投放到該地區(qū) ![]() 萬件(不包含積壓商品),要保證每月都滿足供應(yīng),
萬件(不包含積壓商品),要保證每月都滿足供應(yīng), ![]() 應(yīng)至少為多少萬件?(積壓商品轉(zhuǎn)入下月繼續(xù)銷售)
應(yīng)至少為多少萬件?(積壓商品轉(zhuǎn)入下月繼續(xù)銷售)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】紅隊隊員甲、乙、丙與藍隊隊員A、B、C進行圍棋比賽,甲對A,乙對B,丙對C各一盤,已知甲勝A,乙勝B,丙勝C的概率分別為0.6,0.5,0.5,假設(shè)各盤比賽結(jié)果相互獨立.
(1)求紅隊至少兩名隊員獲勝的概率;
(2)用ξ表示紅隊隊員獲勝的總盤數(shù),求ξ的分布列和數(shù)學期望Eξ.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ![]() 的圖象過點P(0,2),且在點M(-1,
的圖象過點P(0,2),且在點M(-1, ![]() )處的切線方程
)處的切線方程 ![]() 。
。
(1)求函數(shù) ![]() 的解析式;
的解析式;
(2)求函數(shù) ![]() 與
與 ![]() 的圖像有三個交點,求a的取值范圍。
的圖像有三個交點,求a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知平面直角坐標系![]() ,以
,以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系,
軸的非負半軸為極軸建立極坐標系, ![]() 點的極坐標為
點的極坐標為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)寫出點![]() 的直角坐標及曲線
的直角坐標及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的中點
的中點![]() 到直線
到直線![]() :
: ![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《九章算術(shù)》是我國古代的數(shù)學名著,書中有如下問題:“今有五人分五錢,令上二人所得與下三人等.問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分5錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數(shù)列.問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,甲所得為( )
A.![]() 錢
錢
B.![]() 錢
錢
C.![]() 錢
錢
D.![]() 錢
錢
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)f(x)=Asin(ωx+φ)(其中 ![]() )的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象( )
)的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象( ) 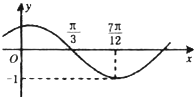
A.向右平移 ![]() 個長度單位
個長度單位
B.向右平移 ![]() 個長度單位
個長度單位
C.向左平移 ![]() 個長度單位
個長度單位
D.向左平移 ![]() 個長度單位
個長度單位
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com