
【題目】已知函數![]() .
.
(Ⅰ)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)若![]() ,求函數
,求函數![]() 的單調區間;
的單調區間;
(Ⅲ)若![]() ,求證:
,求證: ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)證明見解析.
;(Ⅲ)證明見解析.
【解析】試題分析:(Ⅰ)求出![]() 求出
求出![]() 的值可得切點坐標,求出
的值可得切點坐標,求出![]() 的值,可得切線斜率,利用點斜式可得曲線
的值,可得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(Ⅱ)在定義域內,分別令
處的切線方程;(Ⅱ)在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(Ⅲ)
的減區間;(Ⅲ) ![]() ,等價于
,等價于![]() ,等價于
,等價于![]() ,設
,設![]() ,只須證
,只須證![]() 成立,利用導數研究函數的單調性,利用單調性求出
成立,利用導數研究函數的單調性,利用單調性求出![]() 的最小值,證明最小值大于零即可得結論.
的最小值,證明最小值大于零即可得結論.
試題解析:(Ⅰ)若![]() ,則
,則![]() ,
,![]() ,
,
所以![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅱ)![]()
令![]() ,則
,則![]() .
.
令![]() ,得
,得![]() (依題意
(依題意![]() )
)
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
所以, ![]() 在區間
在區間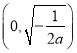 上單調遞減,在區間
上單調遞減,在區間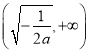 上單調遞增,所以,
上單調遞增,所以, 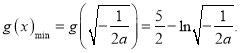
因為![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]() .
.
所以函數![]() 的單調遞增區間為
的單調遞增區間為![]() .
.
(Ⅲ)由![]() ,等價于
,等價于![]() ,
,
等價于![]() .
.
設![]() ,只須證
,只須證![]() 成立.
成立.
因為![]()
由![]() ,得
,得![]() 有異號兩根.
有異號兩根.
令其正根為![]() ,則
,則![]() .
.
在![]() 上
上![]() ,在
,在![]() 上
上![]()
則![]() 的最小值為
的最小值為![]()
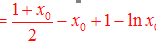
![]()
又![]()
所以![]() 則
則![]()
因此![]() 即
即![]() 所以
所以![]() .所以
.所以![]() .
.
【方法點晴】本題主要考查利用導數求曲線切線方程以及利用導數研究函數的單調性、證明不等式,屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數,即
處的導數,即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數不存在,切線方程為
軸平行時,在 處導數不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


科目:高中數學 來源: 題型:
【題目】已知平面內動點![]() 到兩定點
到兩定點![]() 和
和![]() 的距離之和為4.
的距離之和為4.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)已知直線![]() 和
和![]() 的傾斜角均為
的傾斜角均為![]() ,直線
,直線![]() 過坐標原點
過坐標原點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 是交于
是交于![]() ,
, ![]() 兩點,求證:對任意
兩點,求證:對任意![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定點![]() ,若
,若![]() 是直線
是直線![]() 上位于第一象限內的一點,直線
上位于第一象限內的一點,直線![]() 與
與![]() 軸的正半軸相交于點
軸的正半軸相交于點![]() .試探究:
.試探究:![]() 的面積是否具有最小值?若有,求出點
的面積是否具有最小值?若有,求出點![]() 的坐標;若沒有,則說明理由.若點
的坐標;若沒有,則說明理由.若點![]() 為直線
為直線![]() 上的任意一點,情況又會怎樣呢?
上的任意一點,情況又會怎樣呢?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() 的參數方程是
的參數方程是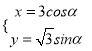 (
(![]() 為參數)以原點為極點,
為參數)以原點為極點, ![]() 軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線
軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() ,
, ![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 和
和![]() 上的任意點,求
上的任意點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提升城市道路通行能力,可為市民提供更多出行便利.我校某研究性學習小組對成都市一中心路段(限行速度為![]() 千米/小時)的擁堵情況進行調查統計,通過數據分析發現:該路段的車流速度
千米/小時)的擁堵情況進行調查統計,通過數據分析發現:該路段的車流速度![]() (輛/千米)與車流密度
(輛/千米)與車流密度![]() (千米/小時)之間存在如下關系:如果車流密度不超過
(千米/小時)之間存在如下關系:如果車流密度不超過![]() 該路段暢通無阻(車流速度為限行速度);當車流密度在
該路段暢通無阻(車流速度為限行速度);當車流密度在![]() 時,車流速度是車流密度的一次函數;車流密度一旦達到
時,車流速度是車流密度的一次函數;車流密度一旦達到![]() 該路段交通完全癱瘓(車流速度為零).
該路段交通完全癱瘓(車流速度為零).
(1)求![]() 關于
關于![]() 的函數
的函數![]()
(2)已知車流量(單位時間內通過的車輛數)等于車流密度與車流速度的乘積,求此路段車流量的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等比數列![]() 的公比為
的公比為![]() ,其前
,其前![]() 項和為
項和為![]() ,前
,前![]() 項之積為
項之積為![]() ,并且滿足條件:
,并且滿足條件:![]() ,
,![]() ,
,![]() ,下列結論中正確的是( )
,下列結論中正確的是( )
A. ![]() B.
B. ![]()
C. ![]() 是數列
是數列![]() 中的最大值 D. 數列
中的最大值 D. 數列![]() 無最小值
無最小值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com