
【題目】今年的國慶假期是實施免收小型客車高速通行費后的第一個重大節(jié)假日,有一個群名為“天狼星”的自駕游車隊.該車隊是由31輛車身長都約為5m(以5m計算)的同一車型組成的,行程中經(jīng)過一個長為2725m的隧道(通過該隧道的車速不能超過25m/s),勻
速通過該隧道,設車隊的速度為xm/s,根據(jù)安全和車流的需要,當0<x≤12時,相鄰兩車之間保持20m的距離;當12<x≤25時,相鄰兩車之間保持( ![]() )m的距離.自第1輛車車頭進入隧道至第31輛車車尾離開隧道所用的時間為y(s).
)m的距離.自第1輛車車頭進入隧道至第31輛車車尾離開隧道所用的時間為y(s).
(1)將y表示為x的函數(shù);
(2)求該車隊通過隧道時間y的最小值及此時車隊的速度.
【答案】
(1)解:∵當0<x≤12時,相鄰兩車之間保持20m的距離;
當12<x≤25時,相鄰兩車之間保持( ![]() )m的距離,
)m的距離,
∴當0<x≤12時,y= ![]() =
= ![]() ;
;
當12<x≤25時,y= ![]() =5x+
=5x+ ![]() +10
+10
∴y= 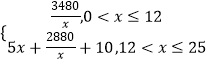
(2)解:當0<x≤12時,y= ![]() ,∴x=12m/s時,ymin=290s;
,∴x=12m/s時,ymin=290s;
當12<x≤25時,y=5x+ ![]() +10≥2
+10≥2 ![]() +10=250s
+10=250s
當且僅當5x= ![]() ,即x=24m/s時取等號,即x=24m/s時,ymin=250s
,即x=24m/s時取等號,即x=24m/s時,ymin=250s
∵290>250,∴x=24m/s時,ymin=250s.
答:該車隊通過隧道時間y的最小值為250s及此時該車隊的速度為24m/s
【解析】(1)利用當0<x≤12時,相鄰兩車之間保持20m的距離;當12<x≤25時,相鄰兩車之間保持( ![]() )m的距離,可得分段函數(shù);(2)分段求出函數(shù)的最小值,即可得到分段函數(shù)的最小值.
)m的距離,可得分段函數(shù);(2)分段求出函數(shù)的最小值,即可得到分段函數(shù)的最小值.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M為線段AD上一點,AM=2MD,N為PC的中點. 
(1)證明:MN∥平面PAB;
(2)求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數(shù)方程為
,其參數(shù)方程為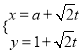 (
(![]() 為參數(shù),
為參數(shù), ![]() ),以
),以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知曲線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ()的焦距為4,左、右焦點分別為
()的焦距為4,左、右焦點分別為![]() ,且
,且![]() 與拋物線
與拋物線![]() :
: ![]()
![]() 的交點所在的直線經(jīng)過
的交點所在的直線經(jīng)過![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過![]()
![]() 的直線
的直線![]()
![]() 與
與![]() 交于
交于![]() 兩點,與拋物線
兩點,與拋物線![]() 無公共點,求
無公共點,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)= ![]() (x>0),數(shù)列{an}滿足
(x>0),數(shù)列{an}滿足 ![]() (n∈N* , 且n≥2).
(n∈N* , 且n≥2).
(1)求數(shù)列{an}的通項公式;
(2)設Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n﹣1anan+1 , 若Tn≥tn2對n∈N*恒成立,求實數(shù)t的取值范圍;
(3)是否存在以a1為首項,公比為q(0<q<5,q∈N*)的數(shù)列{a ![]() },k∈N* , 使得數(shù)列{a
},k∈N* , 使得數(shù)列{a ![]() }中每一項都是數(shù)列{an}中不同的項,若存在,求出所有滿足條件的數(shù)列{nk}的通項公式;若不存在,說明理由.
}中每一項都是數(shù)列{an}中不同的項,若存在,求出所有滿足條件的數(shù)列{nk}的通項公式;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下面四組函數(shù)中,f(x)與g(x)表示同一個函數(shù)的是( )
A.f(x)=|x|, ![]()
B.f(x)=2x, ![]()
C.f(x)=x, ![]()
D.f(x)=x, ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某單位共有10名員工,他們某年的收入如下表:
員工編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(萬元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求該單位員工當年年薪的平均值和中位數(shù);
(2)從該單位中任取2人,此2人中年薪收入高于7萬的人數(shù)記為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知員工年薪收入與工作年限成正相關關系,某員工工作第一年至第四年的年薪分別為4萬元,5.5萬元,6萬元,8.5萬元,預測該員工第五年的年薪為多少?
附:線性回歸方程![]() 中系數(shù)計算公式分別為:
中系數(shù)計算公式分別為:
 ,
, ![]() ,其中
,其中![]() 為樣本均值.
為樣本均值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在四棱錐P﹣ABCD中,底面ABCD為矩形,PA⊥平面ABCD,點E在線段PC上,PC⊥平面BDE. 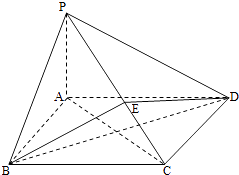
(1)證明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com